机器学习

机器学习-吴恩达老师的视频课学习记录

开始学习机器学习啦！以后研究生研究方向是机器学习、人工智能。现在大四课程基本结束了，提前学习和了解一下机器学习的基础知识。主要目的是入一个小门，为后期研究生课程做个铺垫。加入博客帮助我记录重点，不至于刷完视频跟啥都没学一样…再而，大家在看到这些内容时，有什么不同的理解也可以相互讨论。有错误欢迎指出~~😘

什么是机器学习？

机器学习的定义

Arthur Samuel（“ 机器学习之父 ”）对于他的定义是：计算机可以在没有明确编程下进行学习。

机器学习的分类

$$机器学习=\left\{ \begin{matrix} 监督学习(Supervised Learning) \\ 无监督学习(Unsupervised Learning) \end{matrix} \right.$$

监督学习

Part 1

监督学习的定义：给定输入X与正确答案（输出Y），在模型从输入X与正确答案（输出Y）中学习。经过训练与学习之后，当给出一个全新的输入x时，他能够尝试给出正确答案（输出Y）。分析对象为：”输入、输出”，“x到y的映射”。

输出X与正确答案的具体实例你可以从下表中理解：

INPUT X	OUTPUT Y (正确答案)	应用
email	spam? (0,1)	spam filtering
audio	text transcripts	speech recognization
English	Chinese	machine translation
user info/advertising	click? (0,1)	online advertising
image、radar info	position of other cars	self-driving car
image of phone	defect	visual inspection

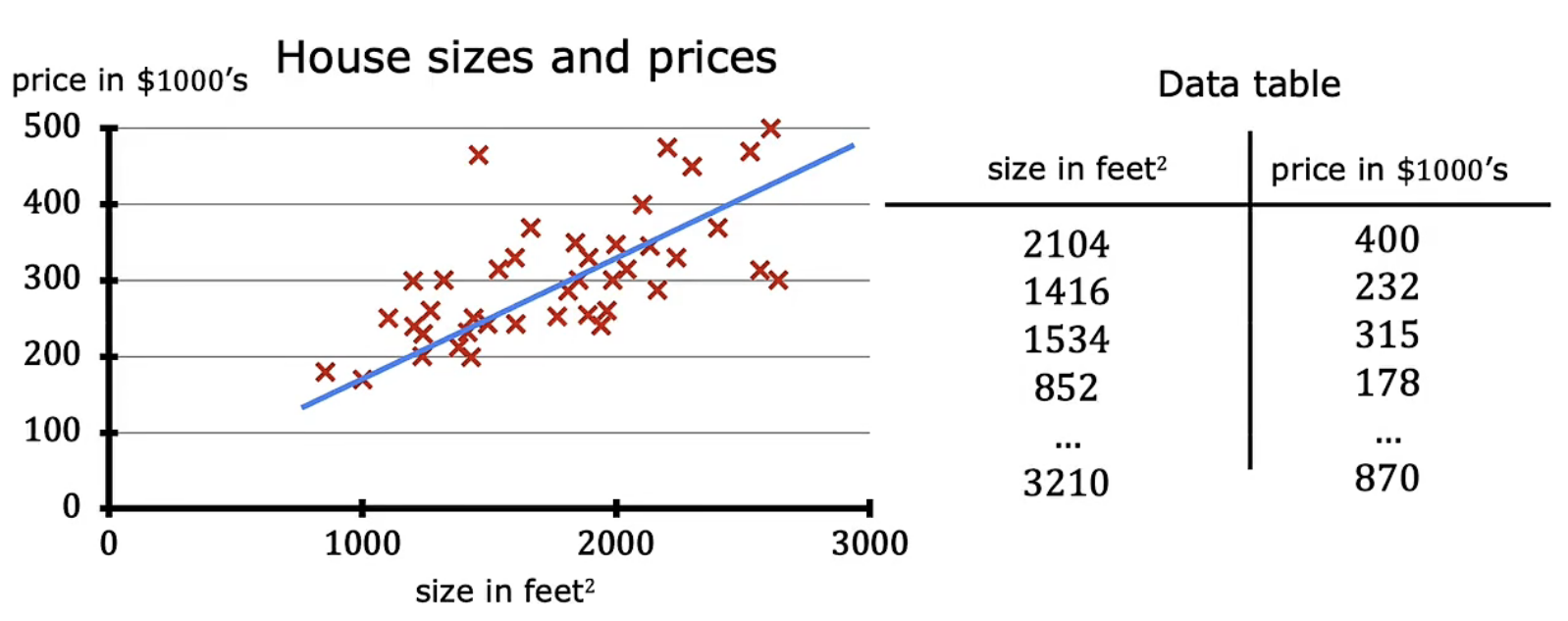
监督学习包括两个主要问题，其中一个问题是回归，回归算法能够达到预测的目的。回归问题的一个例子：

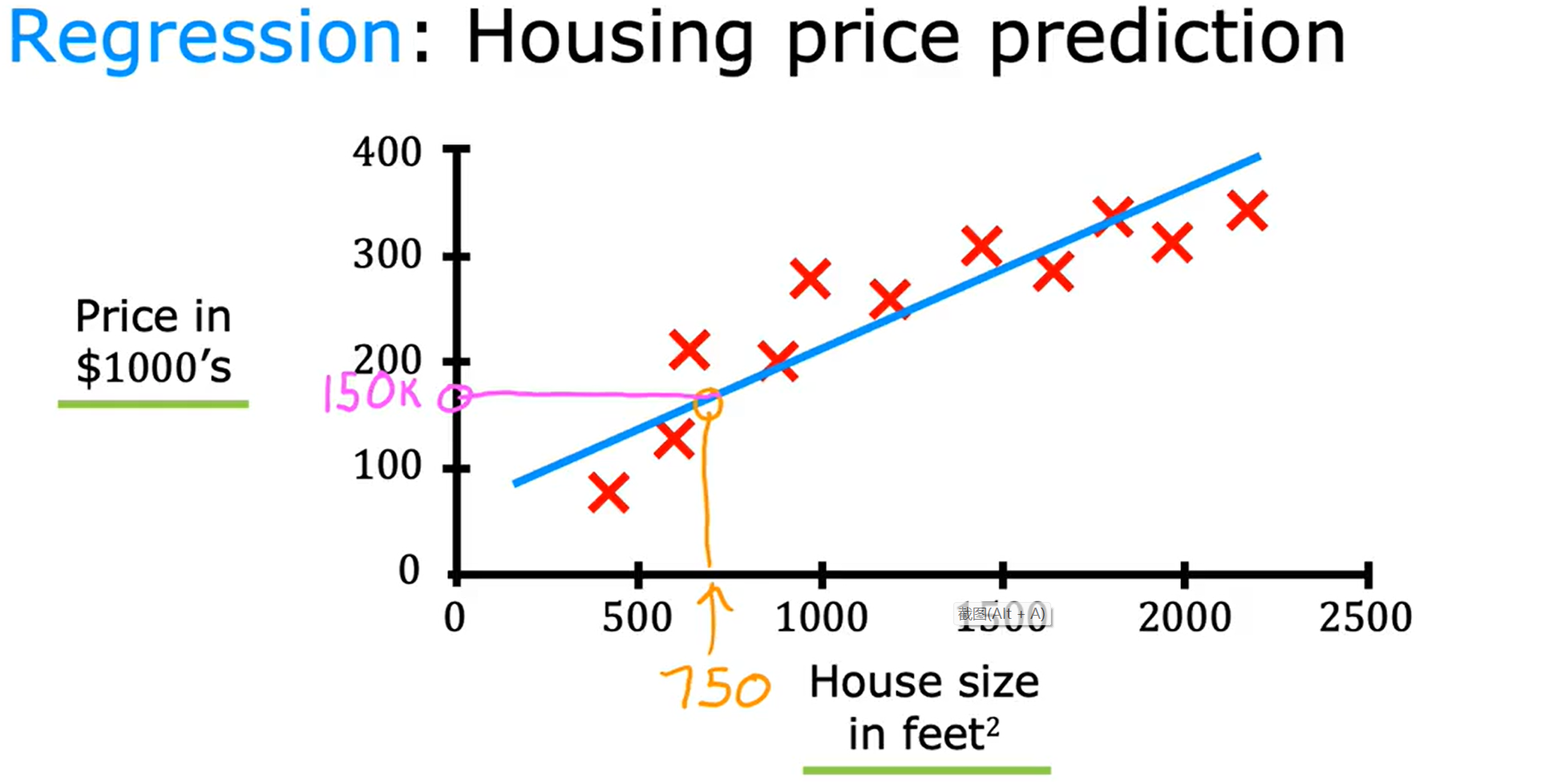
在此图中我们可以看到，x轴是房子的面积，y轴是房子的价格。在此情境下，我们有了输入X和正确答案（输出Y），通过回归算法我们便可以推测其他大小的房子的价格。这个价格取决于我们所选择的回归线，有可能是一元的、二元的、n元的等等。此处，我认为这里的问题是一个简化模型，实际问题考虑到地区、房子类型肯定更复杂。这里只是为了帮助我们理解回归。

---

Part 2

第二种主要的机器学习算法是：分类算法。

与回归不同的是，分类仅仅预测一小部分的数据，输出为两个，1或0。有时也会是超过两个结果的有限个数输出。而回归则是尝试预测无限多的可能中的一个。我们可以分类数字，动物，肿瘤等等。

$$监督学习=\left\{ \begin{matrix} 回归(Regression)\\ 分类 (Categories)\end{matrix} \right.$$

在Part1中我们提到，监督学习需要一个输入X，但其实我们可以有多个输入X。

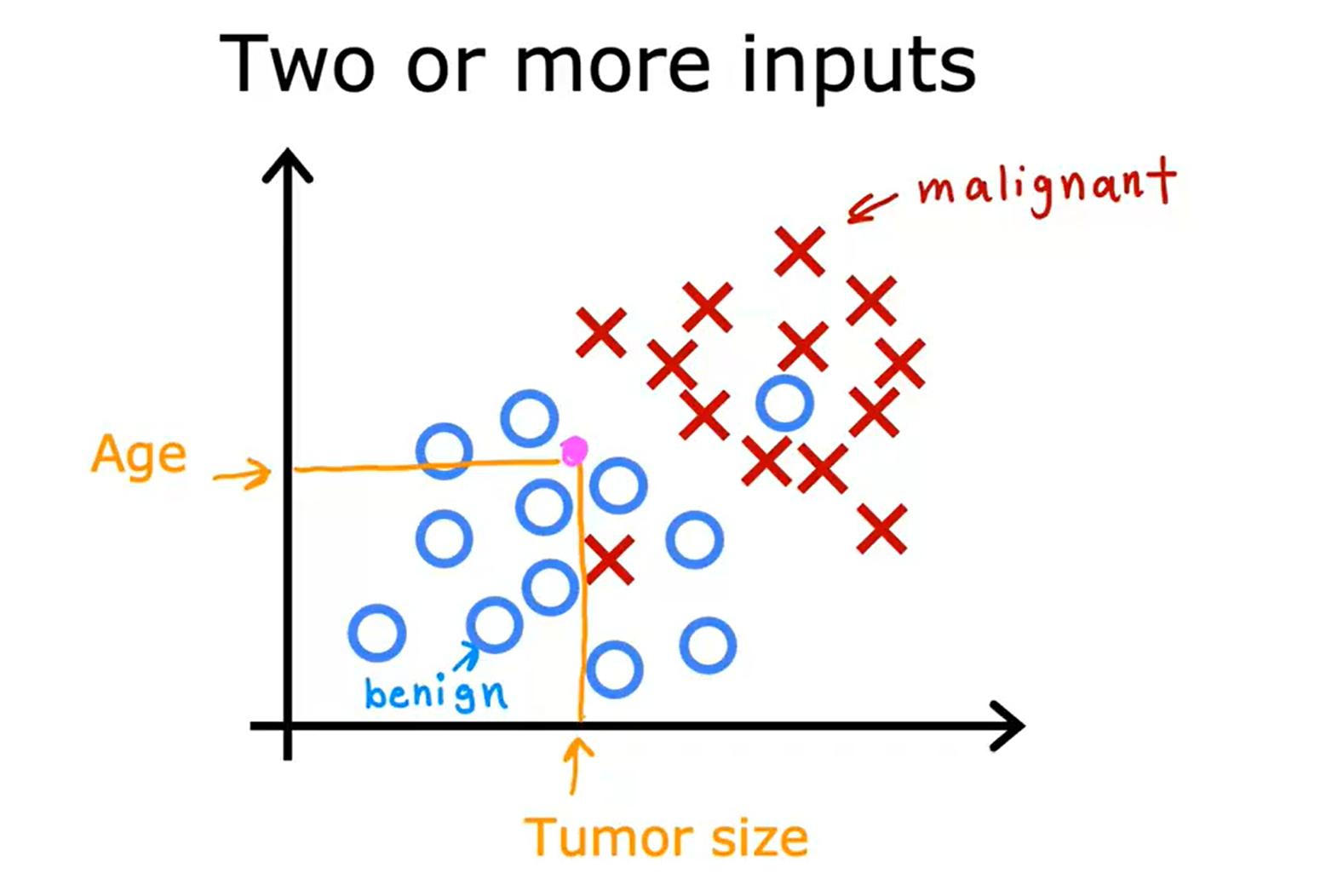
在上述分类恶性或良性肿瘤的例子中，学习算法可能要做的是找到一个分界线，这个分界线需要很好的拟合我们现在拥有的数据库。

---

无监督学习

无监督学习的定义：相比于监督学习，无监督学习没有正确答案（输出Y），只有输入X这些数据，通过这些数据找到数据特点或者结构又或者模式等等。在无监督学习中，我们不需要知道其输出。如在肿瘤的例子中，找到良性或恶性并不是我们的目标，而是通过这些数据得到他们的结构，模式或有意思的东西。

无监督学习的其中一个典型例子是：集群（聚类）算法。其主要目的是进行分类操作。

例子1：

如在我们日常浏览网站新闻的过程中或网购的过程中，我们总会看到一个区域，其主要目的是帮助你发现与你现在所看的这个条新闻类似的新闻，或与你现在所买的东西类似的东西。这就是基于集群算法的分类。

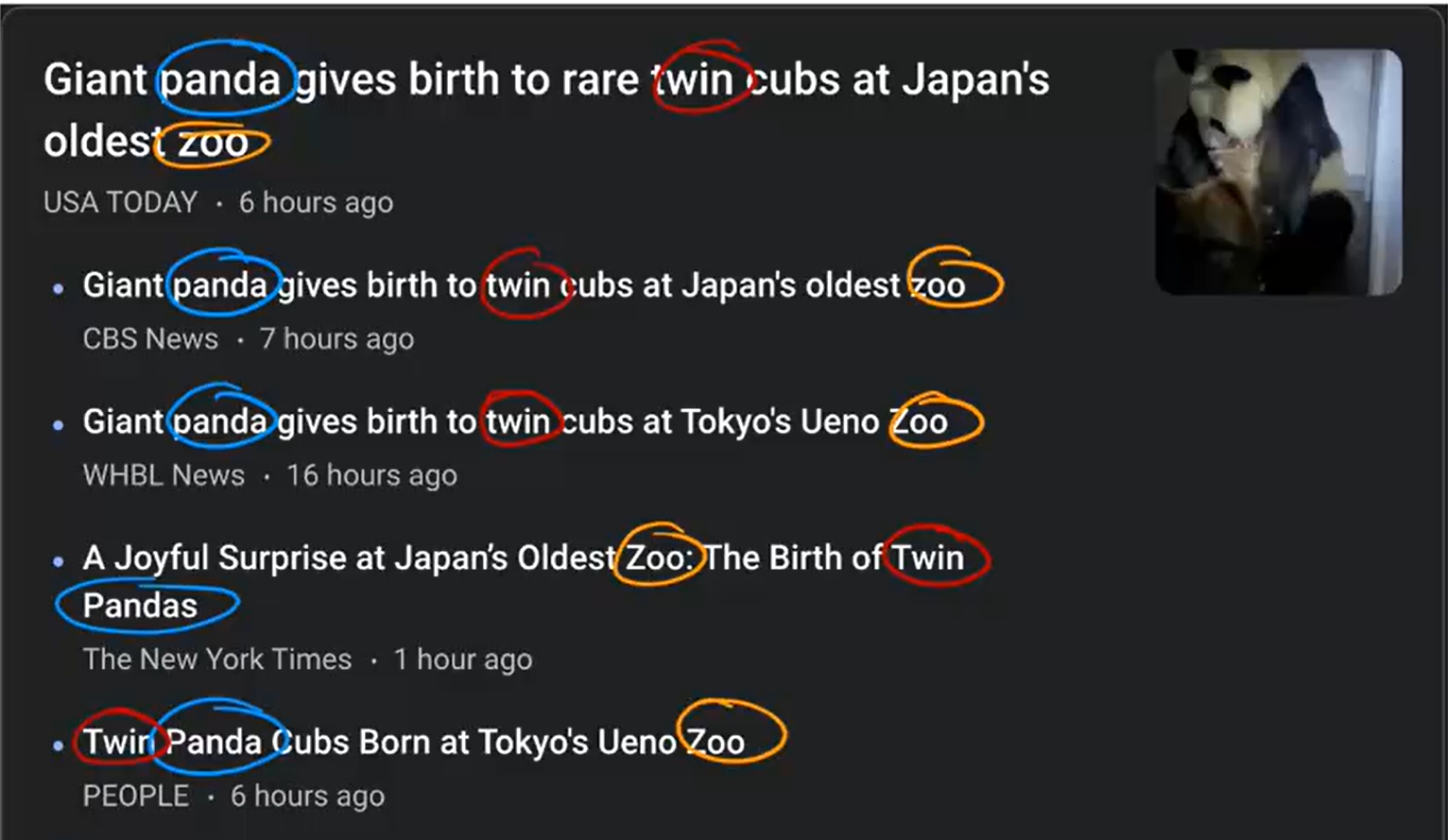
如上图所示，当我们看到一个关于熊猫的新闻时，下方为我们列举了四则类似的新闻（在实际中，他会说“这可能你所感兴趣的” ）

仔细观察我们会发现，下面四则新闻与你所看的新闻有一些共同的词汇：panda，win，zoo。这就有助于你找的你感兴趣的新闻，然后继续进行浏览。

例子2：

对于一个基因库。我们所拥有的数据是大量人的基因序列（输入X），但我们没有标签（输出Y）。在此情景下，无监督学习的任务就是帮我们在这海量基因数据中找的几类人（类型1、类型2、类型3）。在实际中，我们通常会遇到研究表明，爱吃香菜的人与不爱吃香菜的人可能与其基因有关（我就喜欢吃香菜🤭）等等这些常遇到的例子。

例子3：

当一个公司拥有大量用户的信息以及浏览数据时，他们便可以通过集群算法来进行客户分类，如下图：

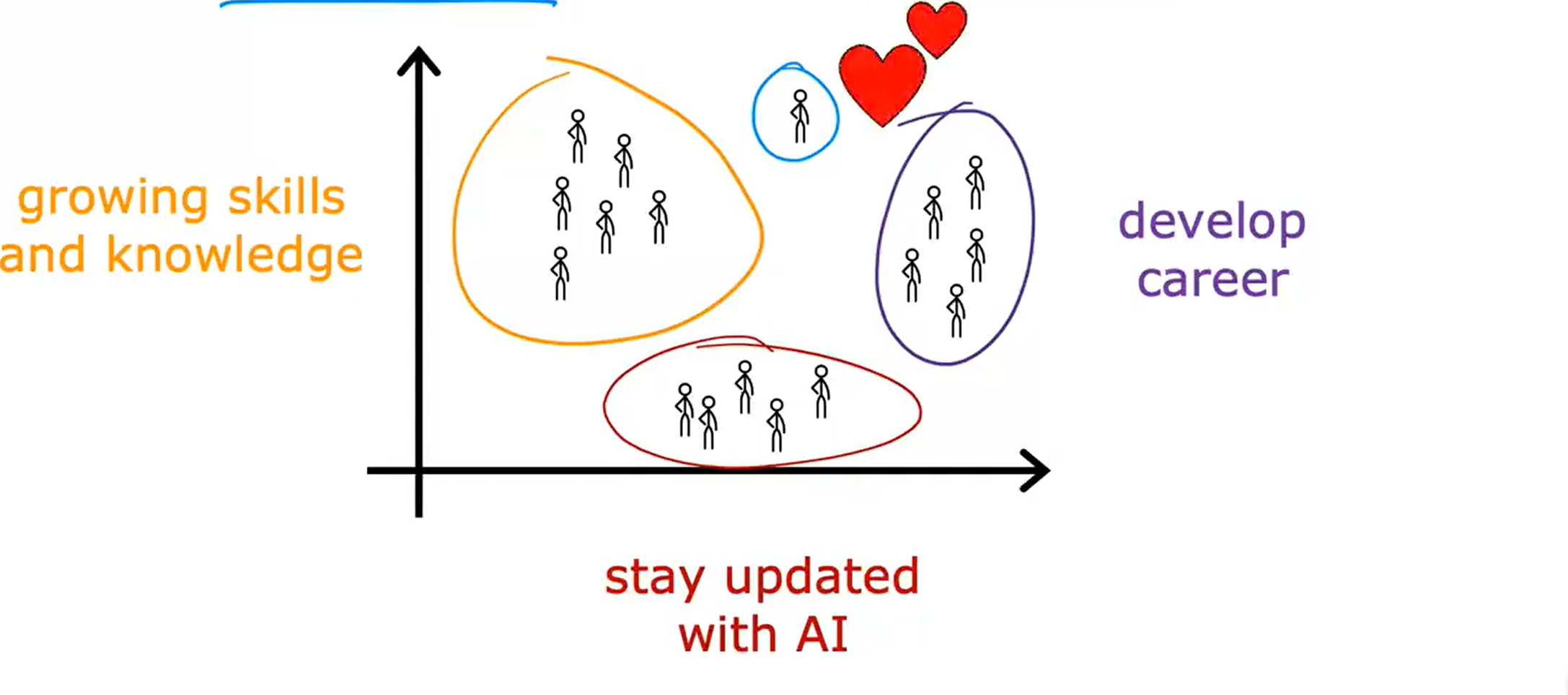
在AI社区中，不同用户加入的目的不同。有些人可能为了增加技能或者知识，有些人为了发展自己的事业，有些人为了关注AI动向。无监督学习便可以通过这些用户数据进行客户分类。有时尽管其可能不是这三个中的任意一个，不过不同担心，因为他也能帮你进行分类，引用吴恩达老师的话就是：

I love you all the same 💕😘

总的来说，无监督学习中的聚类算法能够通过分析海量数据的特点，然后对这些具有相同特点或者结构的数据进行分类。

无监督学习除了集群算法，还有异常检测、降维算法。

---

问题

这里你可能有一个疑问：在监督学习中我们也提到了分类算法，无监督学习中也有也有分类，那他们的区别是什么勒？？

在我的理解看来，监督学习中的分类是提前给出了标签（即正确答案），然后将输入分类给不同的标签。如在动物识别中，我们提前给出了这个动物是狗，那个是猫，另一个是马……给出了一个动物，他会其分给要么是狗或猫又或者马，如果哪个都不是你也可以多设置一个答案（以上都不是），其特点是数据的答案我们已经给出了；而无监督学习则是利用给出的数据，通过分析数据的特点、结构等等，自己进行一个分类，也可以理解为机器自己给出一个”正确答案“，而这些”正确答案“内的数据都符合机器自己总结出的”正确答案“数据特点。

---

这里插播一条链接，昨晚刷抖音看到了剑桥大学发布了一篇关于AI的报告（State of AI Report 2022），大家有兴趣可以看看。

[https://www.stateof.ai/]:

”鼠标点击链接“即可观看🙌

链接好像有些问题，不过点进去直接点back to our site即可。

---

线性回归模型

模型建立

Part 1

在线性回归模型中，一个典型的例子是某个区域对于房价的预测。如下图所示

我们通常知道的数据是房子的面积以及其对应的价格，目标是通过这些数据并利用线性回归模型来预测房价。接下来先介绍一些模型需要使用的符号，帮助我们后续进行模型表达。

符号	含义
x	输入变量特征
y	目标变量
m	训练样本的数量
(x, y)	单个训练样本
(x^(i)^, y^(i)^)	第i个训练样本

Part 2

现在，让我们来建立模型。通过房子面积与价格关系图所示，我们如何找到一条线能够让所有样本点都落在这条线上（当然这在大部分时候是不可能的，我们只能尽量让这些点落在线的附近）。但为了简单起见，我们可以选择一条直线，即一次函数（正如图中所示）。理解了一次函数的拟合有助于我们后续进行复杂曲线的拟合。模型如下：

$$f_{w,b}(x) = w*x+b\tag{1.1}$$

式子(1.1)所表明的就是线性回归模型（Linear Regression），更具体的说这是一个单变量线性回归模型（Univariate linear regression）。式子中的w与b是此模型的参数，他们影响了直线在坐标轴上的位置。

在后续的例子中，我们也会学到多变量线性回归模型，因为就这个房价预测模型来说，面积一定不是影响房价的唯一标准，除了面积可能还会有卧室数量、房龄、周边商场数量等你所能想到的一系列标准。

---

成本函数

成本函数需求：有了模型，我们肯定需要一个标准来衡量一个模型的好坏。那么如何确定这个标准是什么呢？

首先，让我们回归建立此模型的初心：能够让这条直线准确的预测房价。为了完成这个目标，我们希望这条直线能够尽量离每一个样本点都很近（理想情况是每一个样本点都落在我们的直线上，但这显然不可能）。我们知道，在Part2中我们建立了线性回归模型，在该模型中，改变w与b的值将会改变直线在坐标轴中的位置，也就改变了直线与样本点在坐标中的相对位置。因此，w和b的取值对于衡量模型的好坏便尤为重要。

如何用数学符号与公式来实现我们的目标？

1. 想要让直线上的某一个点距离样本点很近，在数学表达式中我们可以写作

$$\hat y ^{(i)} -y^{(i)}\tag{1.2}$$

式子中的 $\hat y^{(i)}$ 代表第i个模型预测值，$y^{(i)}$ 代表第i个样本点目标值。

1. 为了消除值的正负带来的影响我们将式子平方

$$( \hat y ^{(i)} -y^{(i)})^2\tag{1.3}$$

1. 同时考虑所有样本,做求和与平均值操作

$$\frac{1}{2m}\sum_{i=1}^{m}( \hat y ^{(i)} -y^{(i)})^2\tag{1.4}$$

式1.4便是我们衡量模型好坏所用到的公式，我们将其称为成本函数（Cost function），也叫做平方误差成本函数，因为式子中用到了模型预测点与样本点目标值的误差以及平方处理。成本函数用 $J(w,b)$ 表示。

根据字面意思我们可以知道，成本函数代表着一个模型的 “成本”（与商品的成本类似，成本越小越好），成本函数值越小模型对于原数据的拟合程度越高。

---

成本函数的完整表示

由于

$$\hat y^{(i)} = f_{w,b}(x^{(i)})\tag{1.5}$$

所以

$$J(w,b) = \frac{1}{2m}\sum_{i=1}^{m}( f_{w,b}(x^{(i)}) -y^{(i)})^2\tag{1.6}$$

在式(1.6)中，有人可能会有疑问，为什么m个数据样本最后的成本函数却是除以2m。在此处简单解释一下这个问题，那就是为了后期计算更加整洁。详细的原因我将会在后面的内容中提到。

关于成本函数，不同的人会使用不同的成本函数来衡量不同模型的准确性。但平方误差成本函数通常更有利于衡量线性回归模型的准确度。

成本函数的理解

成本函数可以衡量在取不同的w和b的值时模型的拟合度。为了实现更好的拟合效果，我们需要做的是在无数的w和b的组合中找到一组w，b值使得 $J(w,b)$ 最小。为了使成本函数的概念更清晰，我们可以将成本函数可视化。在分析复杂的w，b值组合的情况之前，我们可以先将w或b置零，分析一个参数的改变对成本函数的影响。

此处，我们先将b的值置零，分析w值的改变对成本函数的影响。根据式子（1.1）的模型，我们将b置为0，得到如下式子：

$$f_{w}(x) = w*x\tag{1.7}$$

成本函数变为：

$$J(w) = \frac{1}{2m}\sum_{i=1}^{m}( f_{w,b}(x^{(i)}) -y^{(i)})^2\tag{1.8}$$

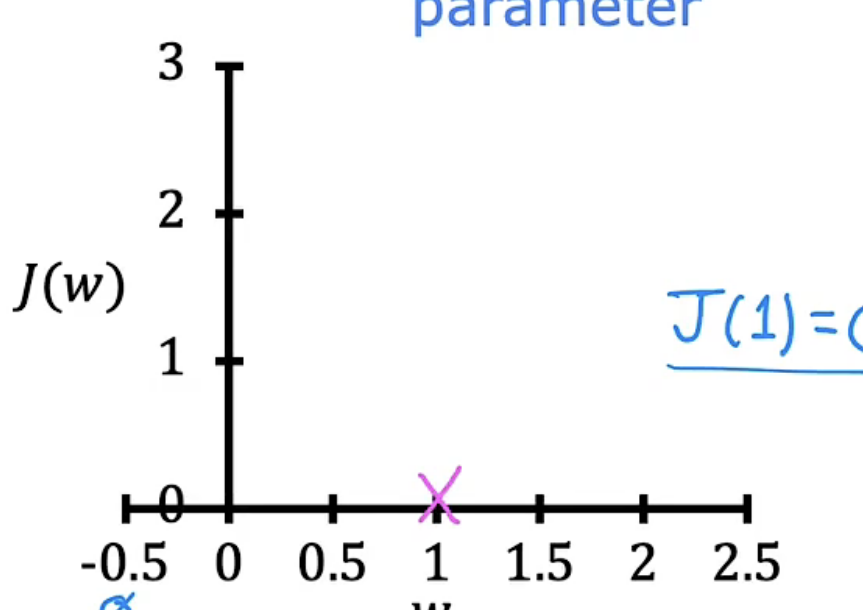
挑选不同的w，计算$f_w(x)$与$J(w)$的值，然后分别绘制图像，我们便可以得到下表图组

w=1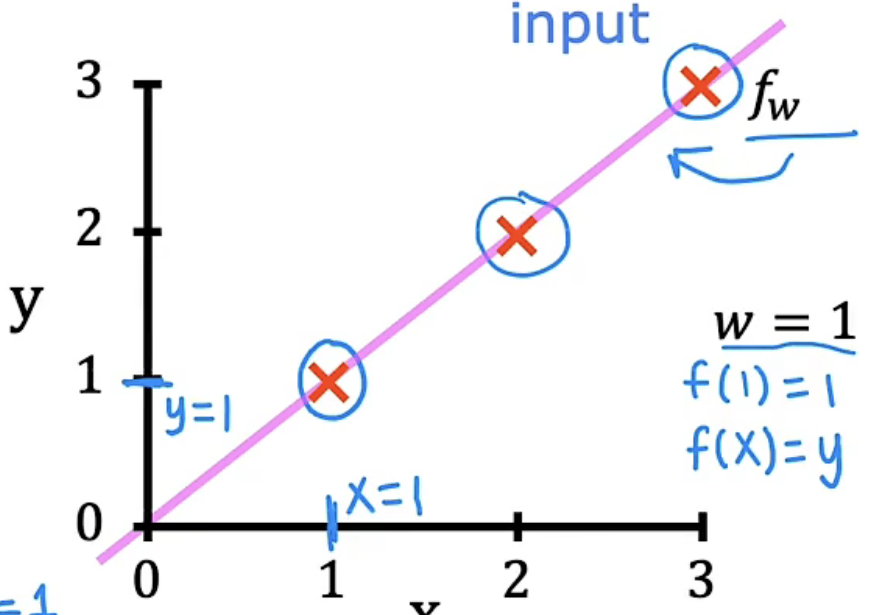
w=0.5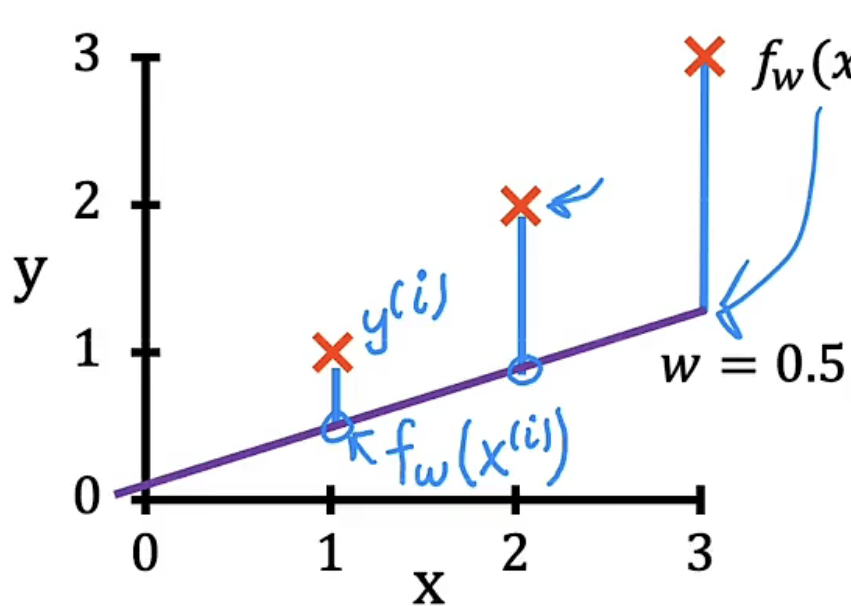
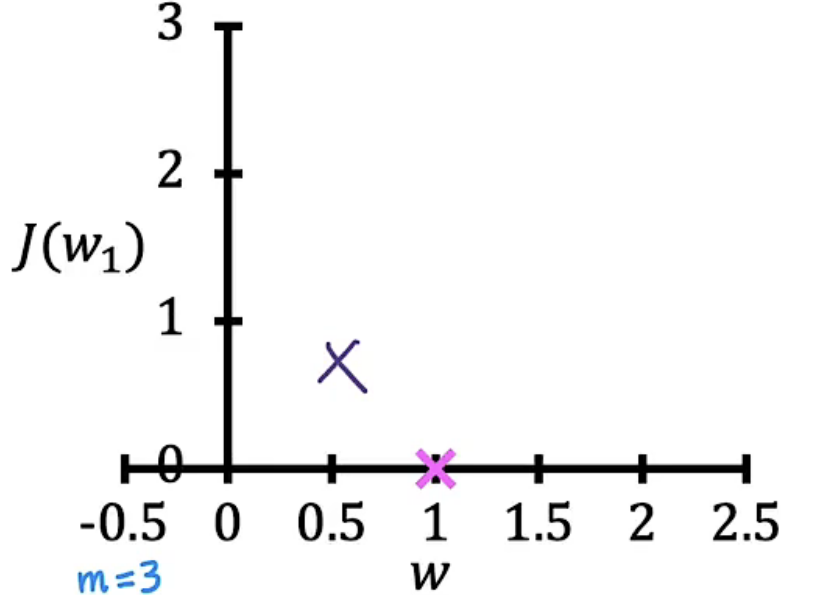w=0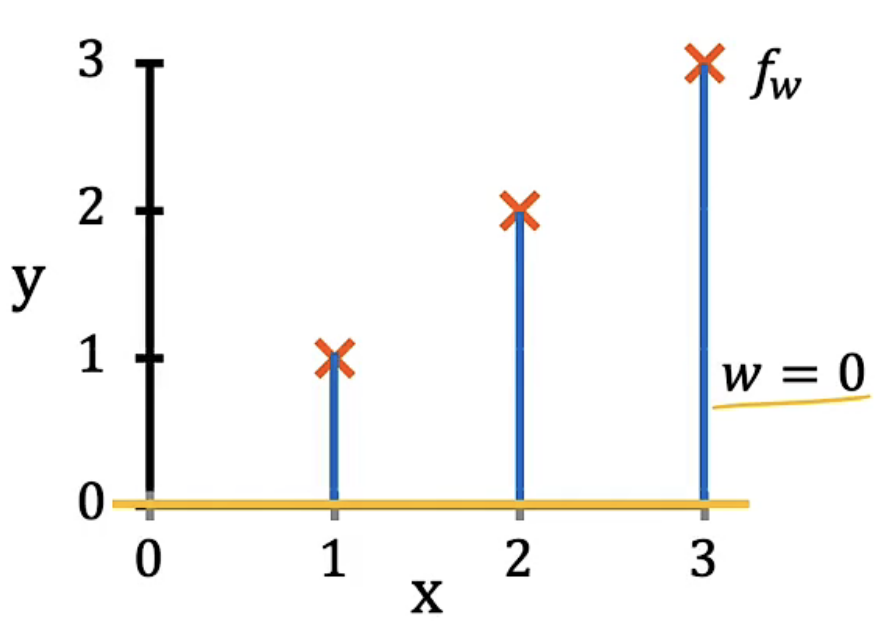
···	···	···
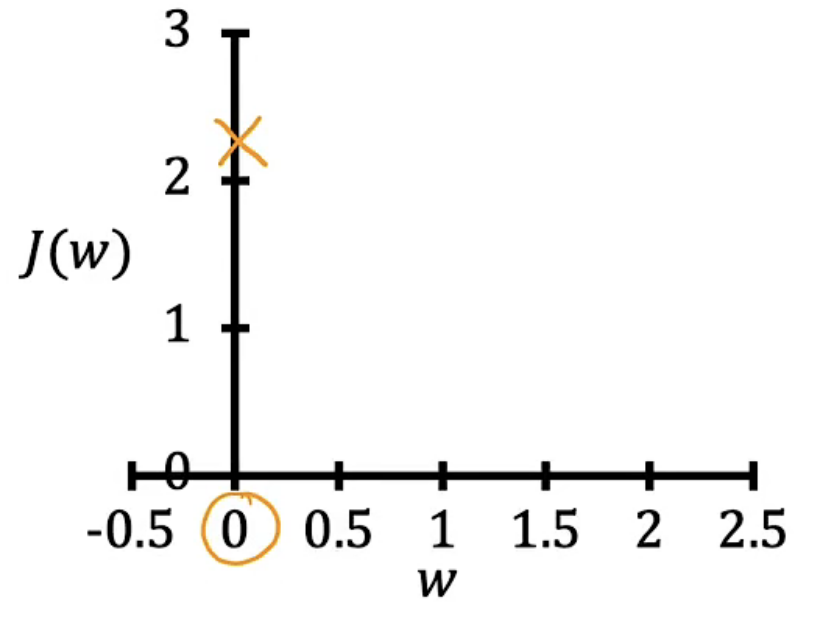所有w	···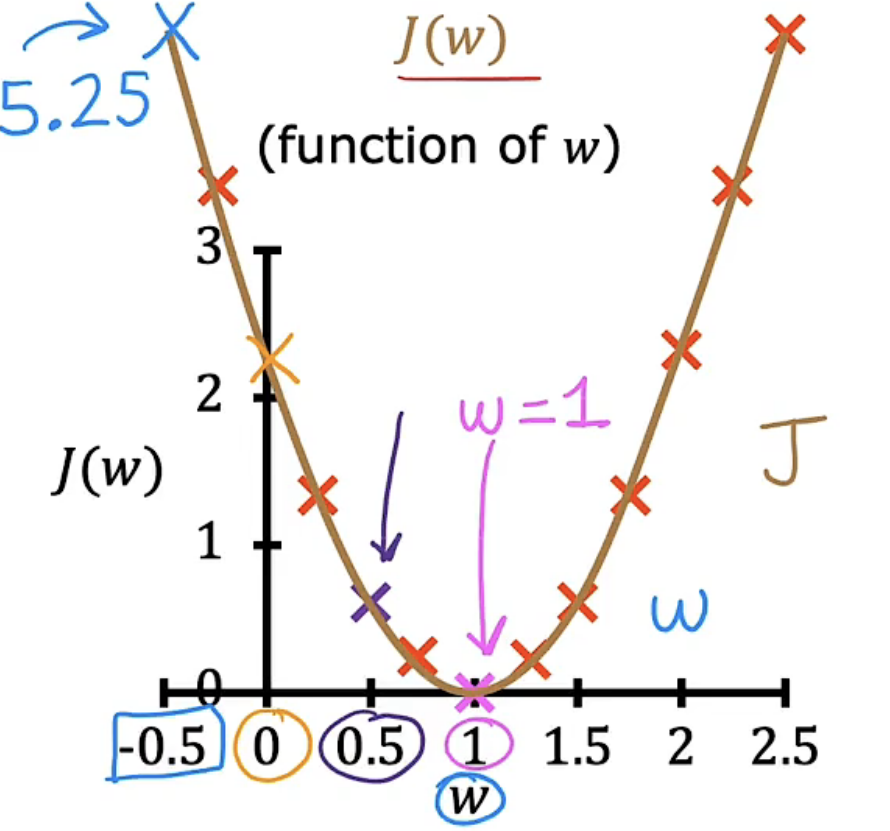

将所有w取值对应的成本函数图像绘制出来可以发现：b等于0时，在w等于1时成本函数值最小，此时直线拟合程度最好。从w=1时，y关于x的坐标图中拟合直线经过了所有的样本点也可以印证此时的w值最优，因为我们的目标就是找到一条曲线能够使其尽量经过所有样本点。

成本函数3D可视化

同理，通过绘图软件的帮助我们可以绘制出$J(w,b)$的图像如下图所示：

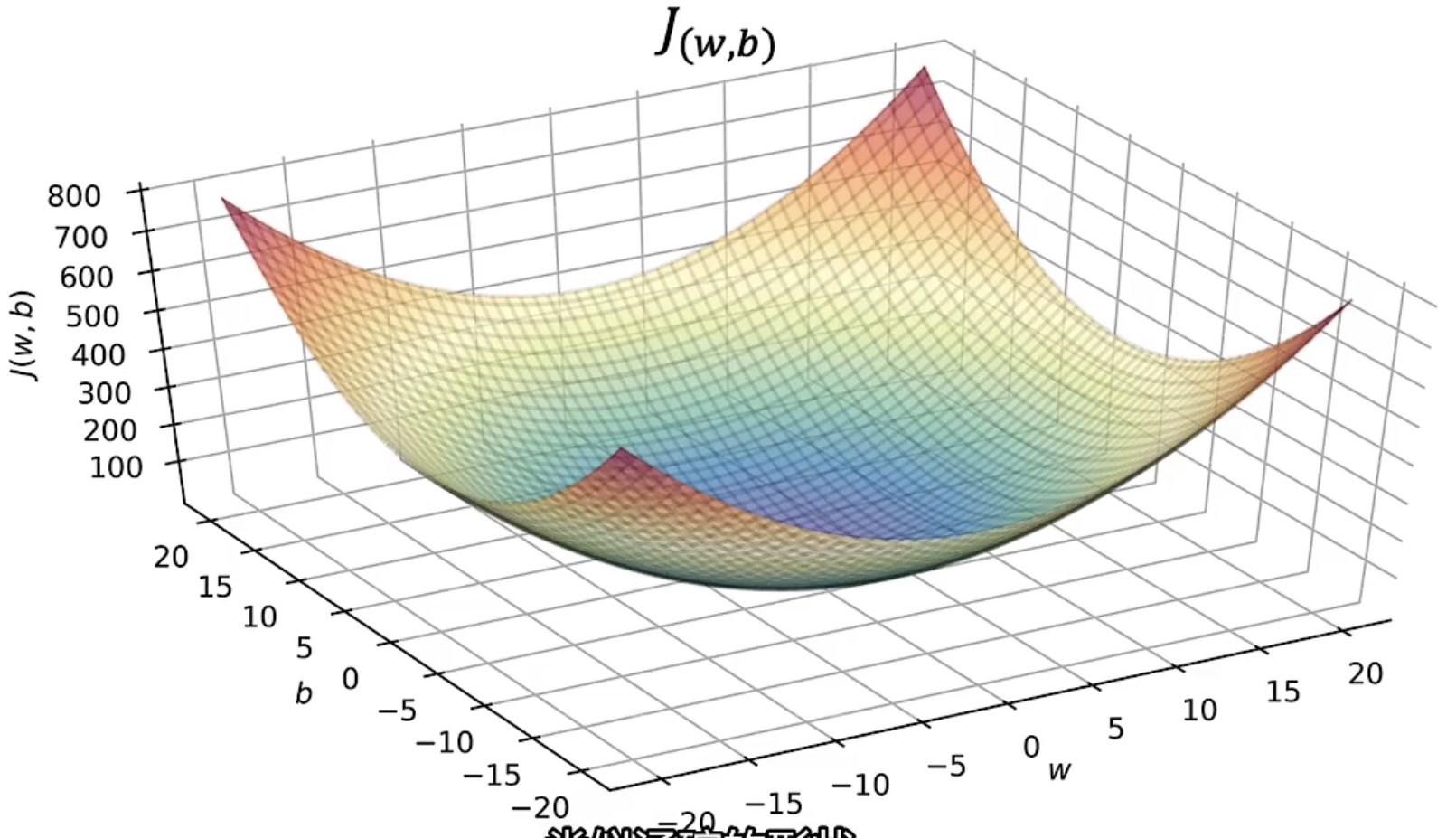
如何理解这张3D图呢？其实我们可以将其与b等于0时的成本函数图结合。当b等于0时，$J(w,b)$关于w的图像呈“U”型，在3D图中我们可以想象在b等于0且平行于w轴的这条线上切割一刀，这个3D立体图形在w，b平面上上的投影是一条U型曲线，这条曲线就是b等于0时$J(w,b)$关于w的图像。可以想象三维图像是b值固定时$J(w,b)$关于w的曲线集合的组合。

除了3D可视化形式，还有另一种简单的可视化形式——等高线图可视化

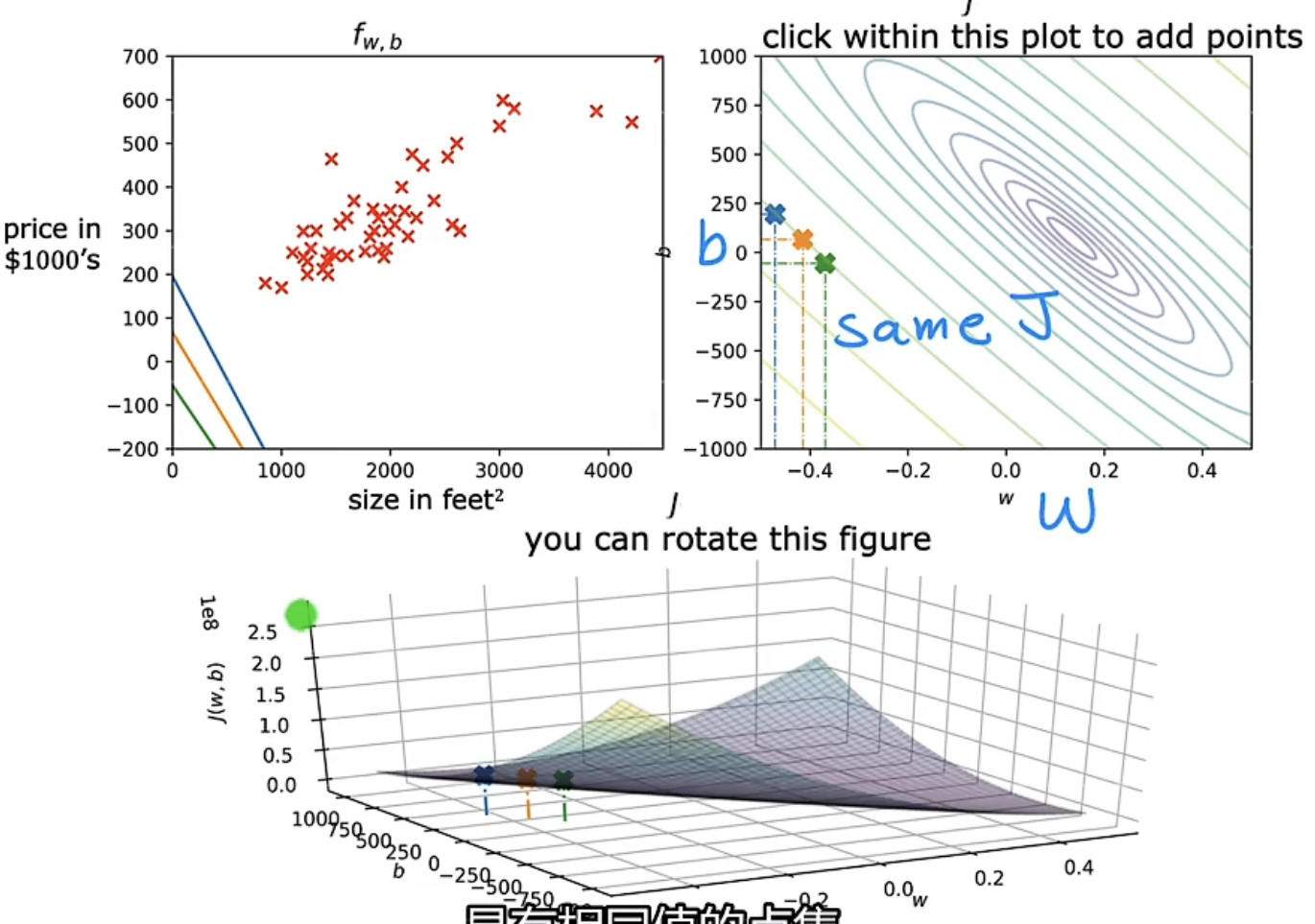
解读：第一行右边的图是第二行的3D图的等高线形式，在同一个椭圆上的$J(w,b)$值相等，不同的椭圆表示不同的$J(w,b)$值。越小的椭圆$J(w,b)$值越小，且其中心点处代表$J(w,b)$值最小。

无论是3D可视化图还是等高线图，都可以帮助我们找到使成本函数最小的w，b组合。但这在更复杂的机器学习中是不现实的，我们需要做的是通过算法和代码找出使成本函数最小的w，b组合。

下面所讲解的方法便是如何通过算法和代码寻找最佳的w，b。

---

梯度下降法

梯度下降法可以用来求解最佳的w、b组合，它也经常用在深度学习中。我们在学习微积分的时候就已经接触到了梯度这个词。在这里我们先引用两句话以便后续更好的理解梯度下降法。

梯度的方向就是函数f(x, y)在这点增长最快的方向

梯度的模为方向导数的最大值

这两句话的推导过程这里先不进行详述，后续需要时会在此补充。

另外，梯度下降法事实上可以用来尝试最小化任何函数，不仅仅是线性回归的成本函数。

理解梯度下降法的实现过程

首先我们可以利用前两节内容构建出模型与成本函数$J(w,b)$，但为了进行更一般的讨论，假设$J(w,b)$是一种更为一般的成本函数，可能拥有多个山峰与多个山谷，如下图所示：

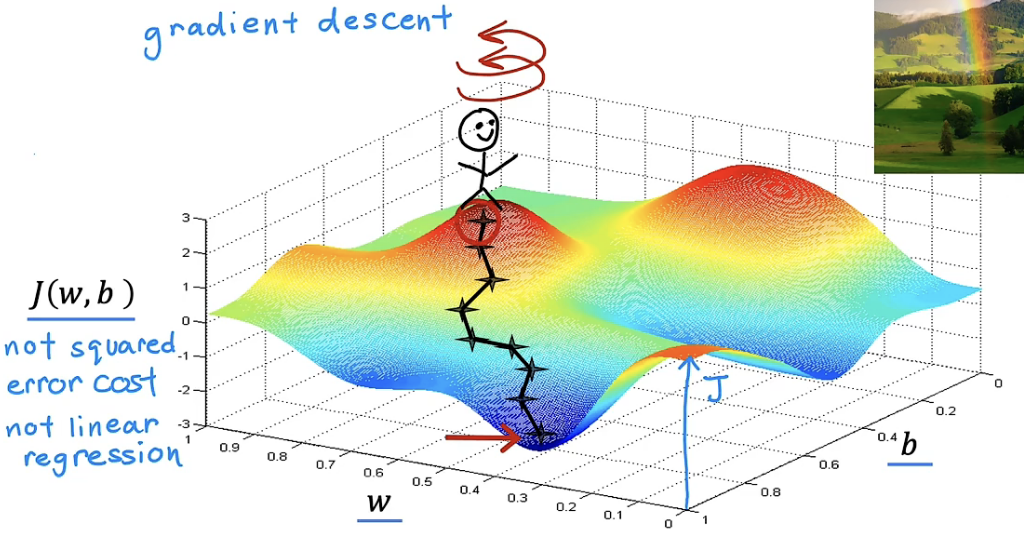
图像中的某个点是成本函数的值，对应了一组w、b值。为了更好地阐述这个过程，你可以先假设你在一个公园里，公园里有许多高高的山坡与低低的山谷。

现在，假设你在一个山峰上，你想要迅速下山，你所做的就是要先环顾四周，找的你认为最陡的一条路（方向），迈出一小步到下一个点。接着在这个新点位，重复刚刚的操作，环顾四周，找到一条你认为最陡的一条路，再迈出一小步，最终你会走到山谷，如上图所示。这个过程其实就是梯度下降算法。

有一点需要说明的是：决定你初始位置的是w、b的初始值，不同的初始值所对应的初始位置便不同，从而会导致不同的 “下山路”，到达不同的山谷。不同的山谷称为 “局部最优解”。

梯度下降法实际算法实现（留存问题）

通过上一节对梯度下降法的理解，我们可以发现梯度下降法有许多小步骤，每个步骤中将会对w与b进行更新，更新的公式如下:

$$w = w-α\frac{d}{dw}J(w,b)\tag{1.9}$$ $$b = b-α\frac{d}{dw}J(w,b)\tag{1.10}$$

式子中，α称为学习率。学习率有如下几个特点：1.取值范围在0-1之间，可以是非常小的数量级。2.学习率基本上控制了下降时每一步的步伐大小。式子中的导数项决定了你想要朝哪个方向迈步子。

在同时更新的w、b中有一个顺序要求，那就是先将w、b值与导数项学习率的乘积相减，再将相减后的值分别赋予新的w和b，如下图

在此节中我留存一个问题：那就是w、b的更新公式中学习率与导数项的乘积的具体含义是？或者说为什么将每次更新所需要减小的值是成本函数的导数项？

梯度下降算法的理解

本节着重于讲解学习率与倒数项的作用，以及为什么利用相乘来更新w、b。这也是上一节中留存的问题！！

为了更方便理解导数项的意义，我们先将模型进行简化，毕竟单变量往往比多变量更容易理解问题。因此，我们先将b设置为0，此时的成本函数变为$J(w)$。在此前我们曾探讨过成本函数$J$关于w的函数图像，如下图

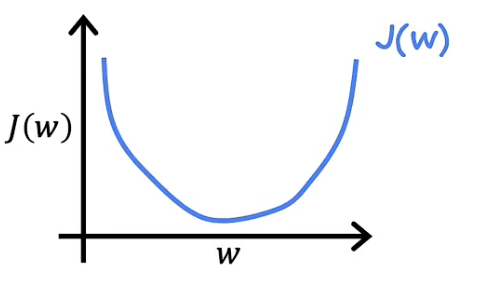
此时先取某一个$w_1$值，假设其大于使成本函数最小的$w$值，此时的$w_1$位于$w$右侧。将该点标注与图像上如下图

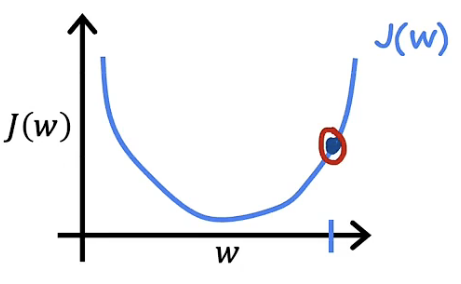
现在讨论导数项的含义，某点的导数值一般表示为该点处函数的切线，我们可以假设斜率是2，如下图

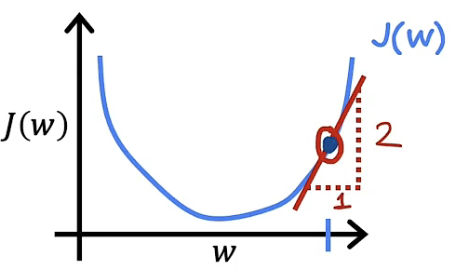
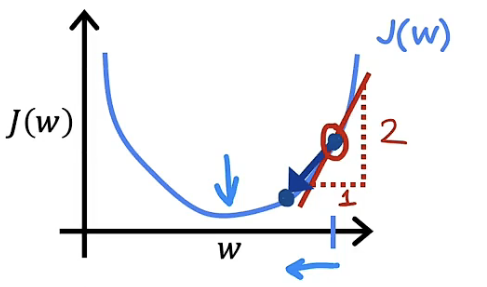
此时，由于 α 大于0，$\frac{d}{dw1}J(w1)$同样大于0，所以$α\frac{d}{dw1}J(w1)$乘积大于0，w1的值减小并朝向使成本函数最小的$w$值趋进与更新。如下图所示

同理，当$w_1$值小于使成本函数最小的$w$值，此时的$w_1$位于$w$左侧。将该点标注与图像上如下图

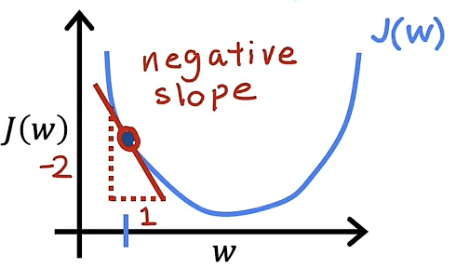
由于 α 大于0，$\frac{d}{dw1}J(w1)$同样小于0，所以$α\frac{d}{dw1}J(w1)$乘积小于0，$w1$的值增加，但同样朝向使成本函数最小的$w$值趋进与更新，如下图

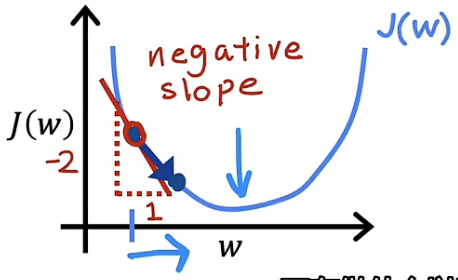
通过上述的分类讨论我们能够发现，导数项的意义在于能够使现有的$w$值朝向使成本函数最小的$w$值趋进与更新。这也印证了吴恩达老师在关于“梯度下降法实际算法实现”这一节中提到的导数项的意义是决定你想要朝哪个方向迈步子。

学习率对梯度下降的影响

学习率会梯度下降效率。为了探讨这个问题，我们同样先简化问题，令b为0。根据w的更新公式（1.9）可知，当学习率太高时，$α\frac{d}{dw}J(w)$将会很大可能导致w的更新直接越过最优w值，甚至导致最终无法收敛。若学习率太低则会影响梯度下降法的执行时间。

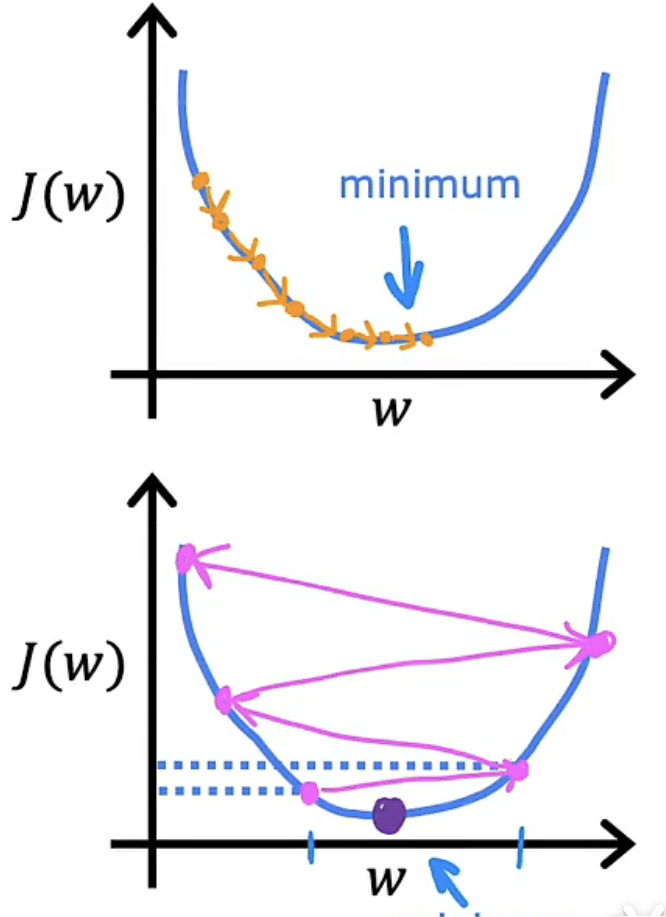
用于线性回归的梯度下降

对于式（1.9）与式（1.10），我们可以计算其导数项表达式并带入，将其进一步简化为如下两个式子：

$$w = w-α\frac{1}{m}\sum_{i=1}^{m}( f_{w,b}(x^{(i)}) -y^{(i)})x^{(i)}\tag{1.11}$$ $$b = b-α\frac{1}{m}\sum_{i=1}^{m}( f_{w,b}(x^{(i)}) -y^{(i)})\tag{1.12}$$

在前几节所讨论的成本函数并不是线性回归模型中的平方误差成本函数，而是为了帮助我们理解公式所假设的一般成本函数，这种一般成本函数可能会存在多个山峰以及多个山谷，也就是拥有多个局部最优解。但对于平方误差成本函数来说，他只存在一个局部最优解，也是全局最优解。所以，只要我们的学习率选的合适，最后的结果总能收敛。

代码实现

后续补充😁

多维线性回归

背景

回想我们在线性回归模型中给出的典型房价预测例子，其中输入特征为房子面积，目标输出为房价。模型的作用是希望给出任意房子面积后能够预测房子价格。但现实情况是，决定房子价格的不仅仅是房子的面积，往往还包括房子的年龄，房室个数，甚至周边商场、公园、医院的个数。这些也都是能够决定房子价格的重要因素，我们需要将他们考虑在内。若如此，我们的线性回归模型便无法完成预测任务，因为模型仅仅包含一个输入特征，那么如何解决具有n（n>=2）个输入特征的预测任务呢？

多维线性回归可以帮助我们完成这个任务。

多维特征

多维线性回归模型拥有多个输入特征，回归模型相较于单维线性回归模型有所改变。

符号解释

在进行模型建立之前，我们还是先进行一些符号解释，如下表：

符号	含义	示例
$x_j$	第$j$个特征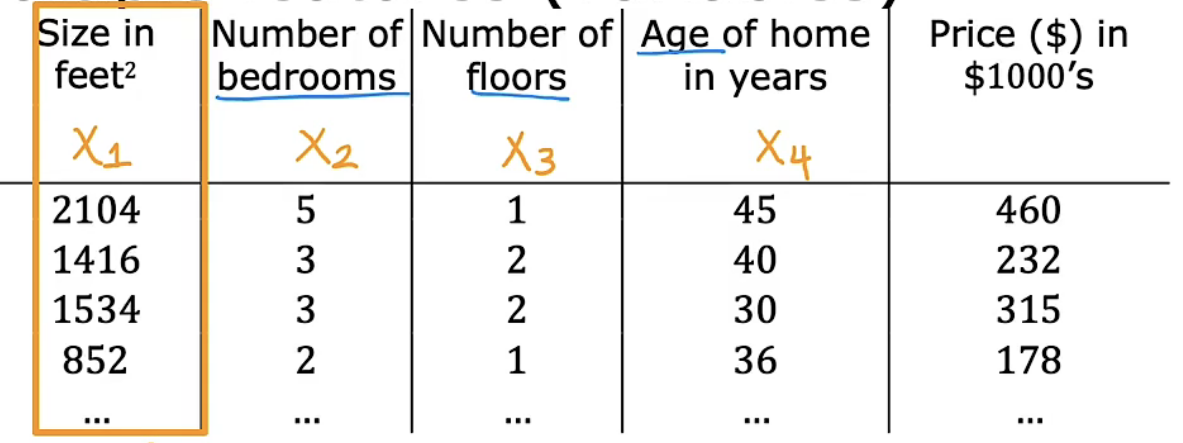
$n$	特征的个数	4
$\vec{x}^{(i)}$	第$i$个训练集的特征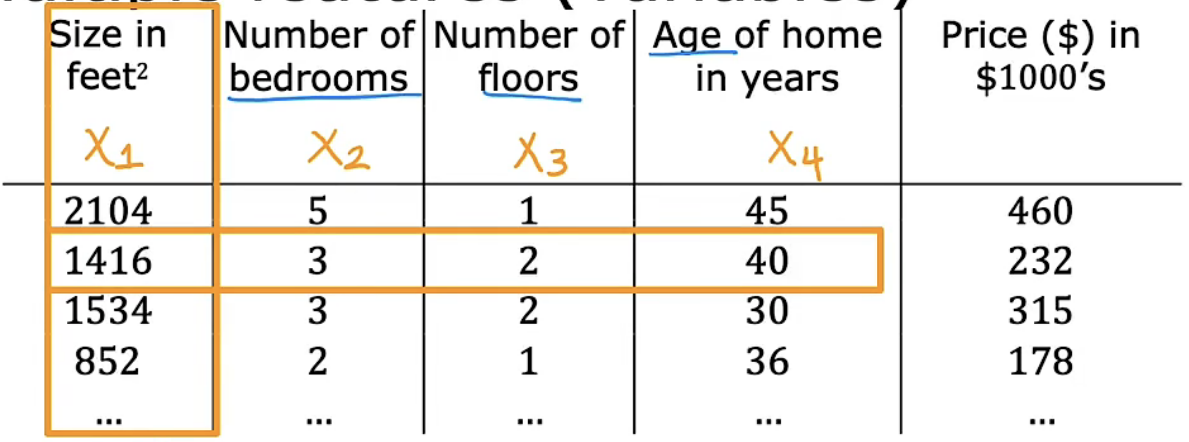
$x_j^{(i)}$	第$i$个训练集的第$j$个特征的值

模型建立

多维线性回归模型如下：

$$f_{w,b}(x) = w_1x_1+w_2x_2+w_3x_3+···+w_nx_n+b\tag{2.1}$$

为了便于理解，我们可以将 $x_1$ 视作每平方米的价格， $x_2$ 视作卧室数， $x_3$ 视作周边商场数等等。

为了简化式子，我们可以将$w_1$-$w_2$视为一个向量（在编程语言中可以用数组代替），记为

$$\vec{w}=[w_1, w_2, w_3, w_4, ··· w_n]\tag{2.2}$$

同样，$x_1$-$x_2$也可以视作一个向量，记为

$$\vec{x}=[x_1, x_2, x_3, x_4, ··· x_n]\tag{2.3}$$

最终，式子（2.1）可以转化为如下

$$f_{\vec{w},b}(\vec{x}) = \vec{w}·\vec{x}+b\tag{2.4}$$

式子（2.4）即为多元线性回归模型。

矢量化

矢量化可以使学习算法更加有效的运行，且代码更加短。矢量化代码将会允许我们使用数值线性代数库，甚至还会用到GPU硬件。GPU硬件可以帮你更快的执行代码，提高并行处理数据的能力。

利用Numpy(借助了并行硬件能力)中如下代码表示模型：

f = np.dot(w,x)+b  

利用上述仅仅一行代码就可以实现点乘操作而不需要使用 “ * ” 与 “ + ” 组合或者for循环，其好处是代码运行速度更快。

在计算机中，使用for循环是一中顺序执行方式，速度慢。但是np.dot(w, x)函数可以先将w数组内的所有w数值与x数组内的所有x数值一步并行的对应相乘。并行计算大大缩短了计算时间。（这也是为什么人工智能专业配置电脑需要好的显卡的原因，因为显卡可以进行并行数据处理。😉）

我回来了。。由于当时有点想赶进度，毕竟遍记边总结速度感觉有点拖，所以从从逻辑回归以后的内容都只记在了纸上，包括神经网络的内容。现在我开始学习决策树模型，同时及时总结。另外，以前的内容我也会抽空慢慢补上，歇了一些日子，也忘了一些东西，当是复习了。

以下的区域用于逻辑回归，神经网络内容的填补

---

---

决策树模型

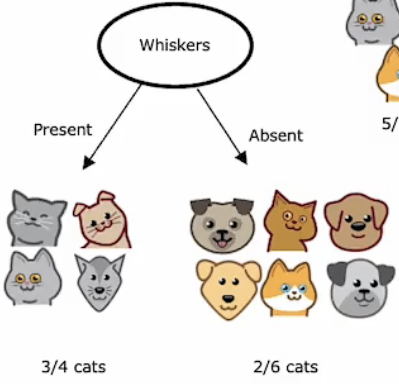
假如我们想要建立一个分类器来区分一个动物是否是一只猫。我们有10个训练集，如下图所示：

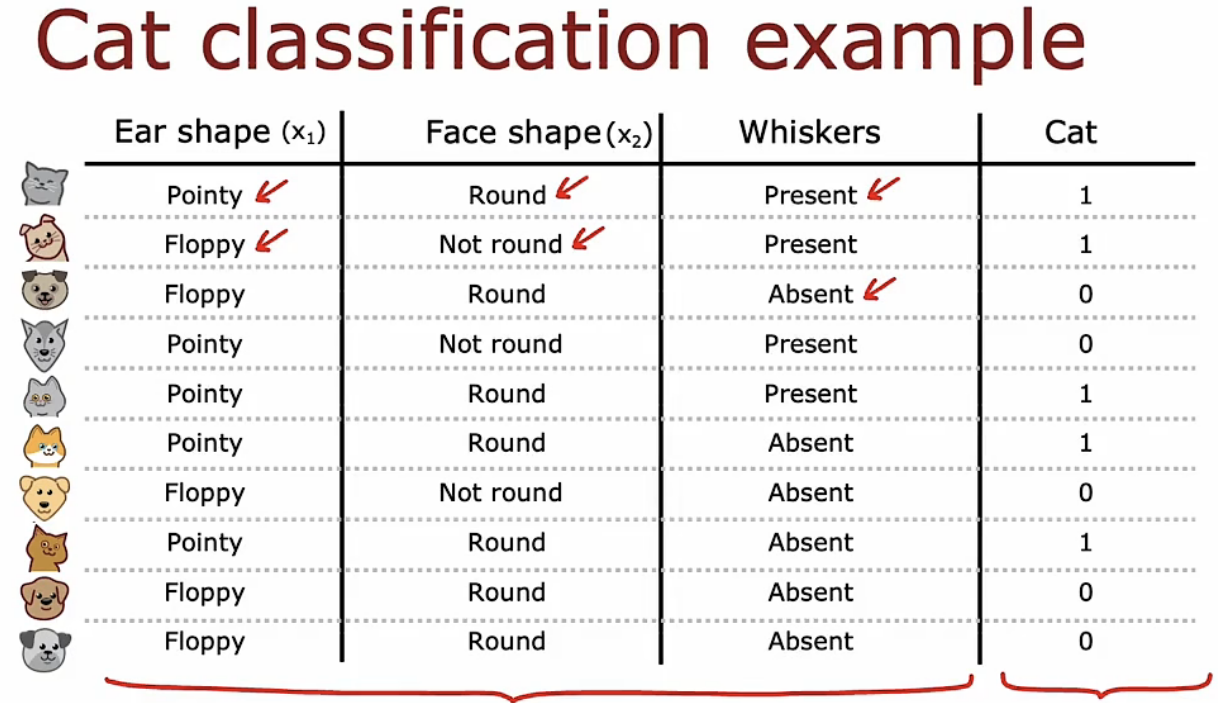
猫的耳朵可能是尖的或者松软的，脸型可能是圆的或是不圆的，胡须可能有可能没有。基于这些特征我们来判断这只动物是否是一只猫。

那么是什么决策树呢？

他就是通过数据集中的特征训练得到一个类似于树状结构的图，从“树“的根部到”叶子“的过程代表着分类的过程。下图就是一个训练后的决策树模型。

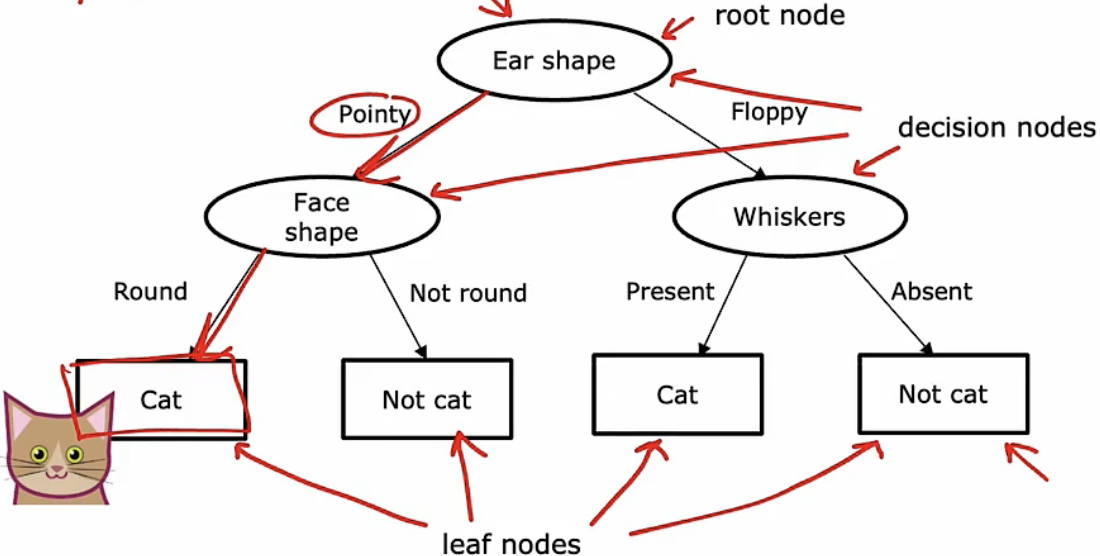
叶子节点是结果的产生，根节点、决定节点分别由分类的特征组成。不同的决策树可能适用于同一个数据集，而这些模型可能有好有坏，所以我们需要找到一个相对准确的模型，它可以很好地适应训练集，同时也要很好的适应交叉验证和测试集来完成预测功能。

决策树中的问题

通过上一节的介绍，决策树模型是通过选择数据集中不同的特征作为根节点，决策节点来实现分类过程。但分析上图中一个已生成的决策树模型后我们可能产生一个问题：

为什么我们选择耳朵形状作为根节点的特征而不是脸的形状以及是否有胡须？为什么右分支的决策节点选择了是否有胡须，而不是和左节点的一样？等等

其实，上面的问题总的来说就是我们是如何决定节点处特征的选择问题的？

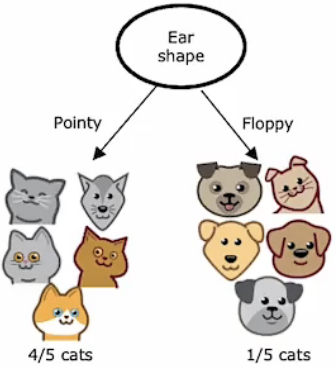
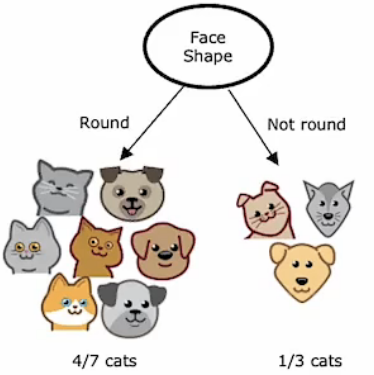
这里，我们提出纯度这个概念。节点处特征的是根据这个节点产生分支的纯度来选择的。在本例子中，假如通过某个节点后，左分支全部是猫，右分支全部是狗，这时我们可以认为这个节点的特征选择是完美的。但在本例子中实际情况并非如此，在选择一个特征作为根节点后，他的左右分支并不能完成分类任务，左分支中仍然有狗，右分支中也仍然有猫，这种情况下，我们可以说他是不纯的。因此，当我们选择不同特征作为根节点时，其左右分支产生的分类结果的纯度是不同的。决策节点的选择同样如此。

上表中所显示的就是当我们选择不同特征作为根节点时，左右分支的纯度对比。所以，在我们选择节点的特征时要根据纯度来选择。尽可能地使经过节点后的分类结果是高纯度的。

这里还有第二个问题：

我们如何决定一个节点何时停止分裂？

1.当一个节点产生的分支纯度为100%。

2.你可以对深度进行限制，当数的最低端达到某一深度时停止分裂。此处深度概念在决策树中表示为从根部到叶子节点的层数，根部节点层数为0，向下一层+1。

3.你也可以对纯度进行限制，当某一节点分裂后纯度达到规定阈值时停止分裂。

4.当一个节点中的例子数低于某一个阈值时停止分裂。

考虑这些问题的原因主要是因为我们要考虑决策树的规模与拟合度问题，当某一个节点分裂后与分裂前的效果几乎相同，但大大增加了决策树的规模与冗杂程度时我们就需要对分裂进行限制，这是我们在上边提出的问题便可以作为参考。

纯度（purity）

在上一节中，我们提到了纯度的概念。那么如何去衡量分类后的纯度是否符合我们的标准呢？为此我们引入熵（Entropy）的概念，熵是衡量纯度的标准。

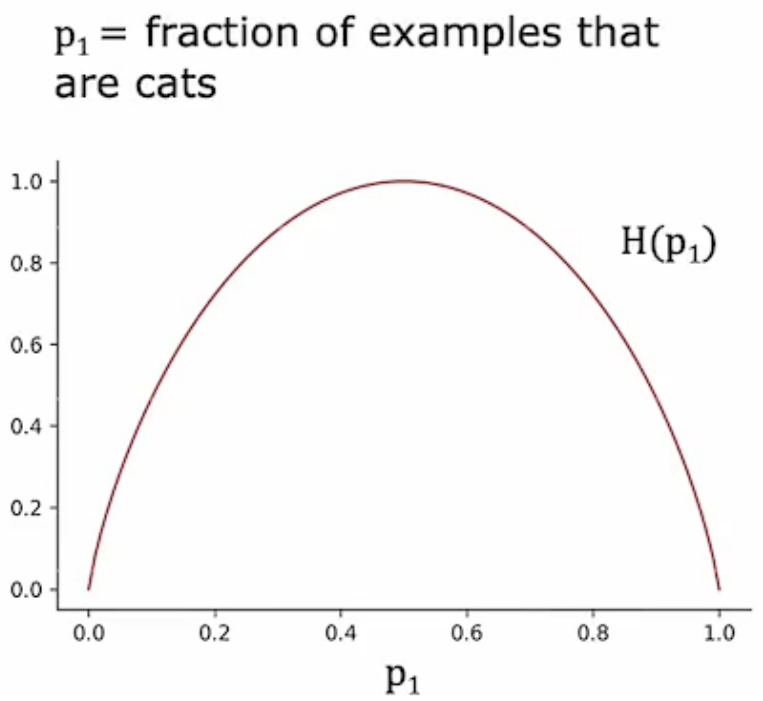
上图所表示的就是熵的函数，横轴为例子中猫的比例，纵轴为熵值。上图中熵的数学表达式定义为：

$$H(p_1)= -p_1log_2(p_1)-(1-p_1)log_2(1-p_1) \tag{4.1}$$

至于为什么选择这个函数作为熵的表达式，我也抱有疑问。不过，吴恩达老师在视频中提到了原因，主要是为了符合在p1为0.5时，函数为一，p1从0.5向0和1靠近时函数值减小，并在0和1处函数值为0。吴恩达老师也提到至于对数函数的底数为啥是2而不是e的原因是为了能够在p1为0.5时等于1，作为一个整数能够在数学上更好解释。

总的来说，熵就是一个取值能够从0到1再到0的函数。另外，其实还有很多函数能够作为纯度标准，比如在一些库中，我们能够见到用Gini值来衡量节点纯度的方法，不过本视频中主要讨论熵的应用。

计算信息增益

在介绍纯度的时候，我们引入熵来作为衡量纯度的标准，熵越小纯度越高。熵的减少被称作信息增益，在本节中我们将介绍如何计算信息增益。在介绍一般的信息增益公式之前，我们还是先借助分类猫的例子来帮助理解信息增益。

在根结点处，不同的特征选择将会导致不同的决策树模型以及左右分支不同的熵。下图中包含了信息增益的计算过程：

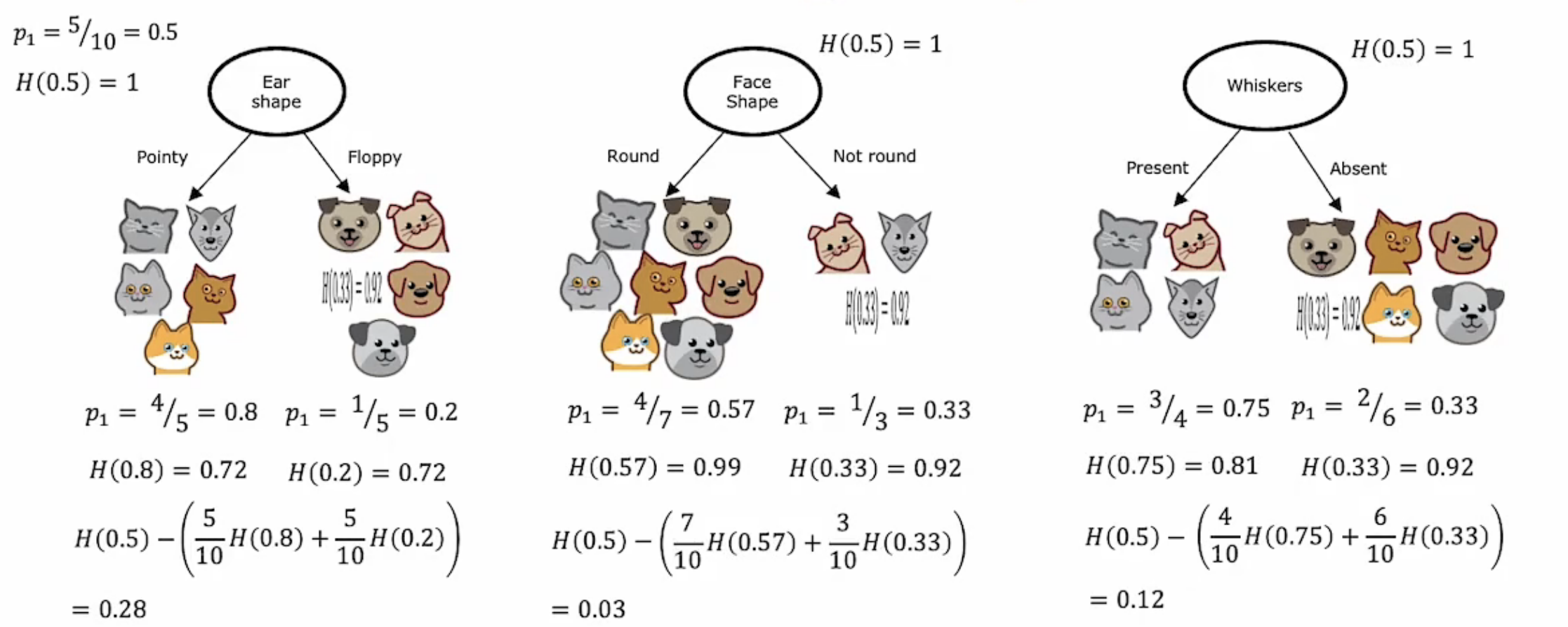
对于不同的决策树，我们利用熵公式分别计算左右分支的的熵值，然后利用加权平均法计算左右分支加权平均后的总熵值。最后，计算出根节点熵值，然后减去经过分裂后的总熵值就能够得到熵减了，也即信息增益。通过上图，我们可以发现根结点处的特征选择不同会产生不同的信息增益。

下面将引入一般公式，但引入公式前我们先介绍几个特殊字符：

特殊符号	注释
$p{_1^{root}}$	根节点处猫的比例
$p{_1^{left}}$	分裂后左分支猫的比例
$p{_1^{right}}$	分裂后右分支猫的比例
$w^{left}$	分裂后左分支例子占总例子数
$w^{right}$	分裂后右分支例子占总例子数

一般公式如下：

$$Information~~gain = H(p{_1^{root}})-(w^{left}H(p{_1^{left}})+w^{right}H(p{_1^{right}}))\tag{4.2}$$

有了信息增益计算方法，我们就可以通过设定阈值来判断决策树是否会过拟合以及是否有必要让节点继续分裂。

决策树模型背后的算法

现在，让我们重头开始，利用例子中的数据集建立他的决策树模型。

第一步：通过计算根节点上不同特征下的信息增益选择根结点处的特征。判断分裂后的左右分支是否符合结束分裂标准，若符合则该分支下的节点停止分裂。

第二步：根节点分裂为左右分支。对于左分支，采用与第一步相同的算法来确定该节点的特征，并确定分裂后的数据是否符合分裂标准，若符合则该分支下的节点停止分裂。右分支同理。

第三步：对于第二步中产生的所有节点使用相同算法确定特征，判断是否符合停止分裂标准…

………..

第n步：直到所有分支下的例子符合停止分裂标准，决策树产生。

通过分析整个过程我们可以发现，生成决策树所使用的其实是递归算法。即对于该函数，在其内部调用该函数本身实现递归。

One-hot热编码

现在，让我们重新回到数据集去，对于一个特征，让我们来思考一下如果一个特征不只有两种情况怎么办？比如对于耳朵形状，除了松软的和尖的，还有一种椭圆的该如何处理？这一节中我们将着手处理这个事情。

对于一个特征包含2个以上的情况时（这里我们记为n个），我们通常采用One-hot热编码来解决。

One-hot热编码 ： 将n种情况分解为n种特征，符合此类特征的值为1，不符合的为0。如下图所示：

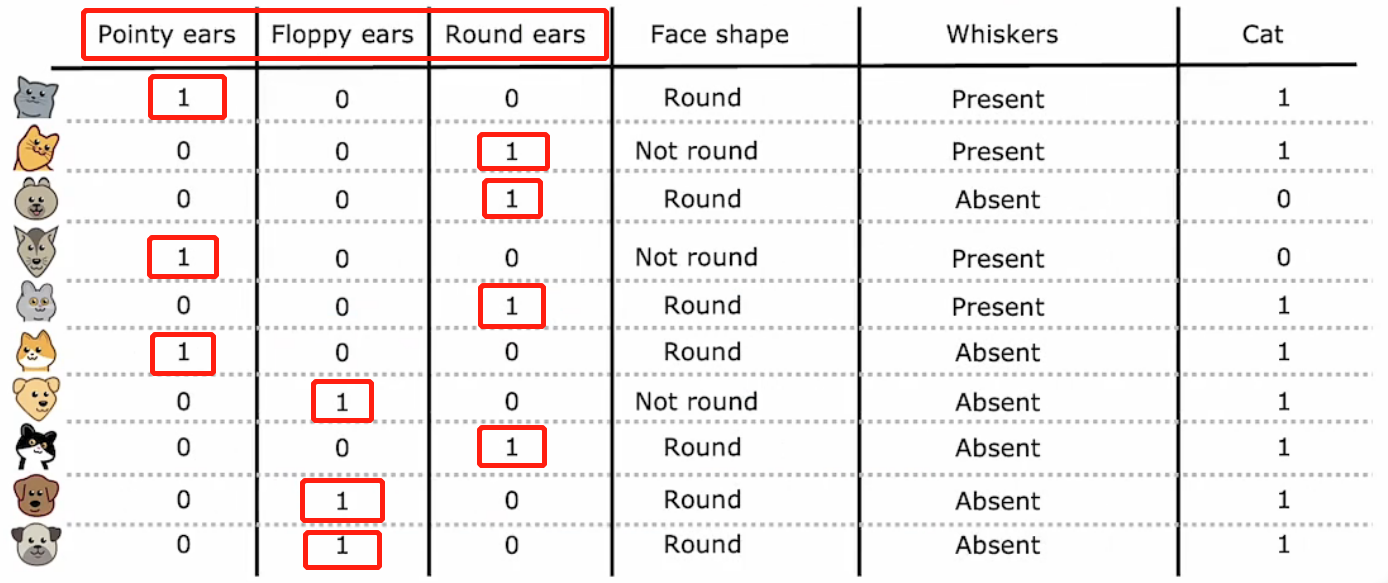
除了分裂后的n个特征外，对于拥有两种情况的特征我们同样也可以进行编码表示：

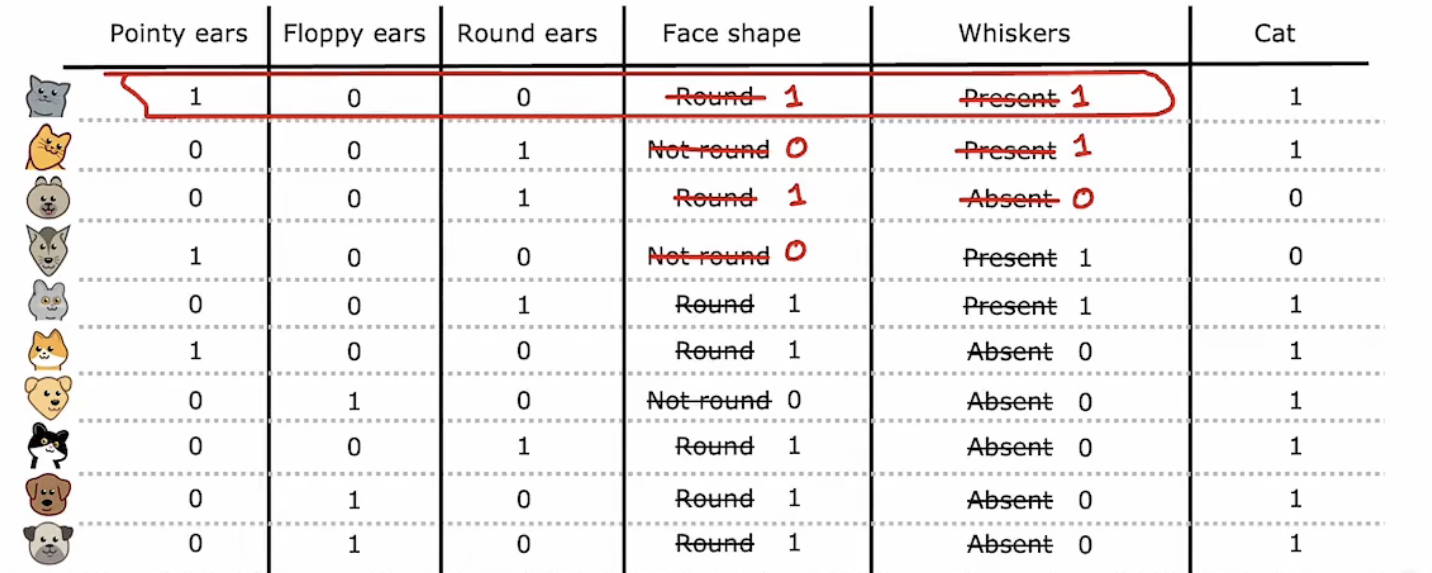
这些编码数据就可以被应用于神经网络训练以及逻辑回归算法中。

有人会联想到那如果是任意数字的连续数值特征呢？我们又该如何处理呢？

对于连续数值我们该如何处理？

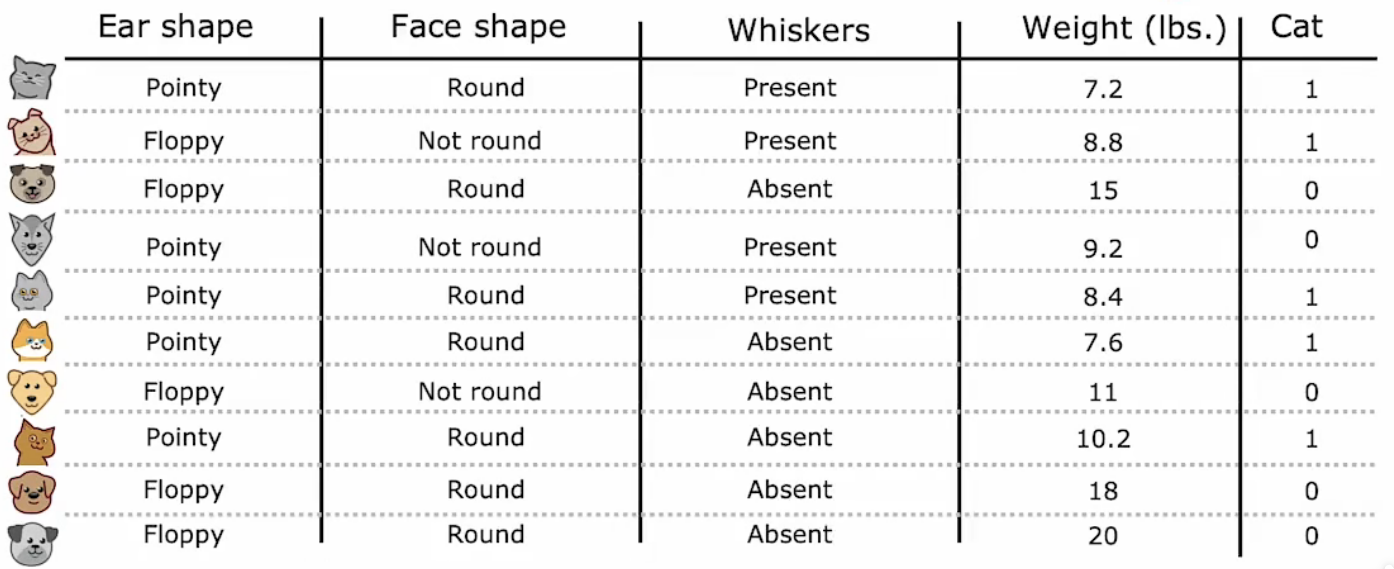
在以前的数据集中我们补充了重量特征，这个重量特征的数值是连续的，此时我们该如何选择一个阈值呢？

对于阈值的选择，我们可以使用与决定节点是否继续分裂时同样的办法。将这些重量特征的数据制图如下：

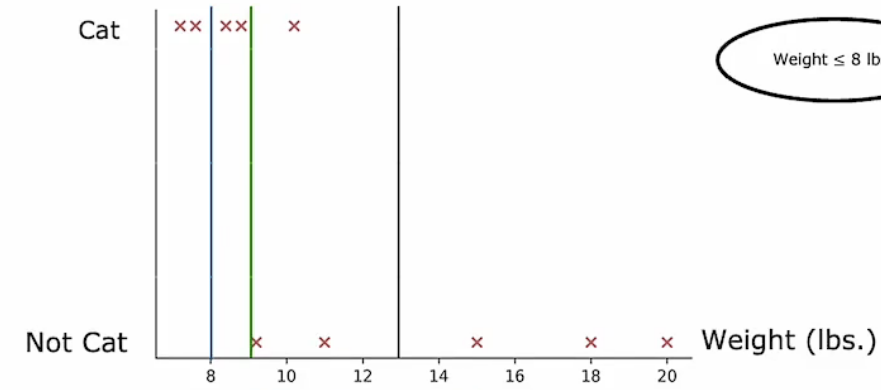
我们可以选择两个临近的数值的中间值进行信息增益计算，在本例子中，一共有十个数据，那么我们就要取九个中间值分别计算他们的信息增益，并比较得出一个最优的阈值。三个示例计算结果如下图：

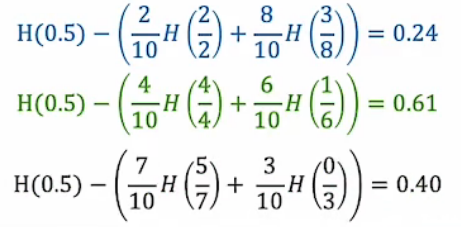
回归树

这节课是一节选修课，其中主要时介绍了如何利用树模型来进行数值的预测，而这个模型由于具有数值预测能力，因此也称为回归树模型。

同样利用分类猫的例子，不过在训练该模型时，数据集的使用发生一点点改变。原来的重量现在作为输出Y，而三种特征仍然作为输入X。

这里需要说明回归树其实我没有很看懂，为什么选择方差作为同衡量纯度时用到的熵一样的标准？有什么依据？这点清楚的可以留言评论哈。

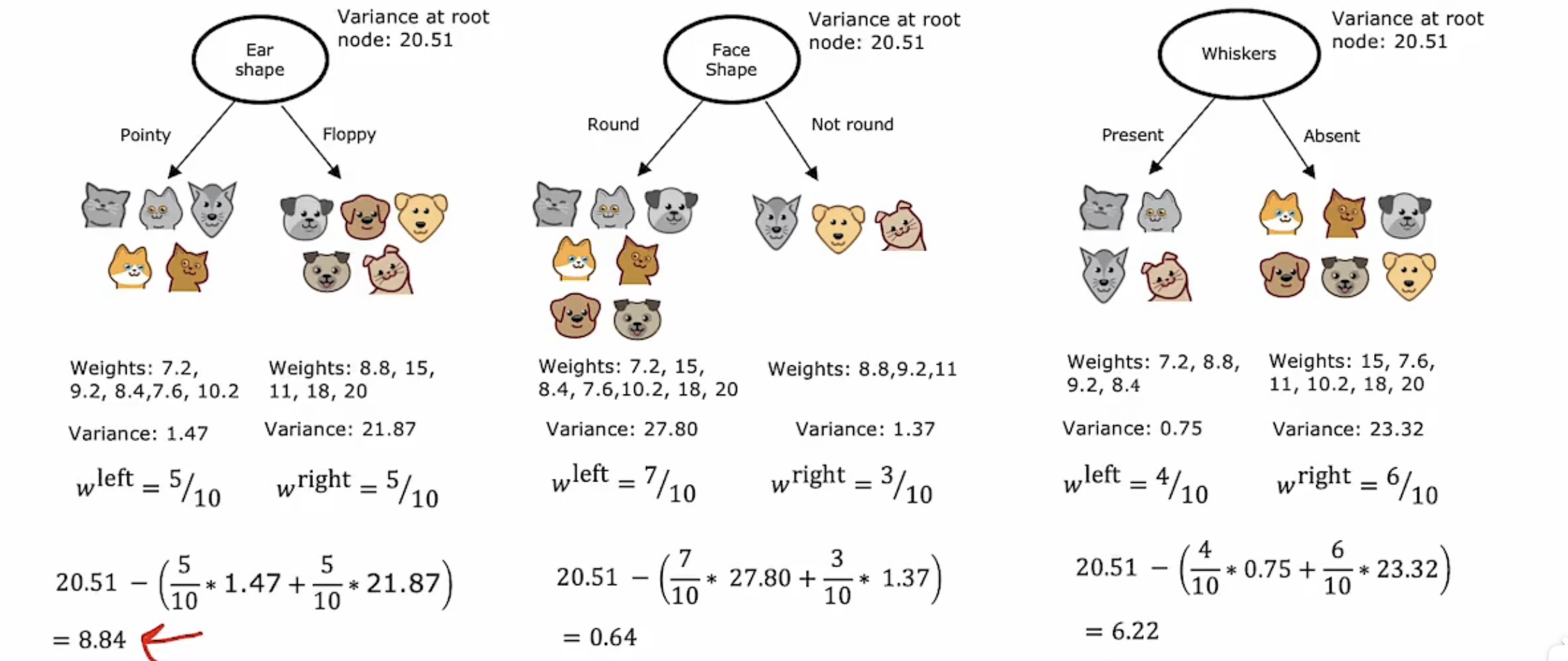
整个回归树的节点建立过程与决策树类似，有变化的地方就是决策树把熵作为衡量纯度的标准，但回归树选择了方差作为衡量数值数据分类是否有预测能力的标准。

使用多个决策树

在使用单个决策树时，通常数据集中的微小变化可能就会导致决策树模型发生大规模改变，训练出来的这种决策树模型就不能很好的适应其他数据。例如，如果我们把十只猫中的其中一只特征变换后就会发现根节点出的特征发生了变化，进而其他节点也会发生变化。

为此，我们解决这个问题的方法是构建多个决策树

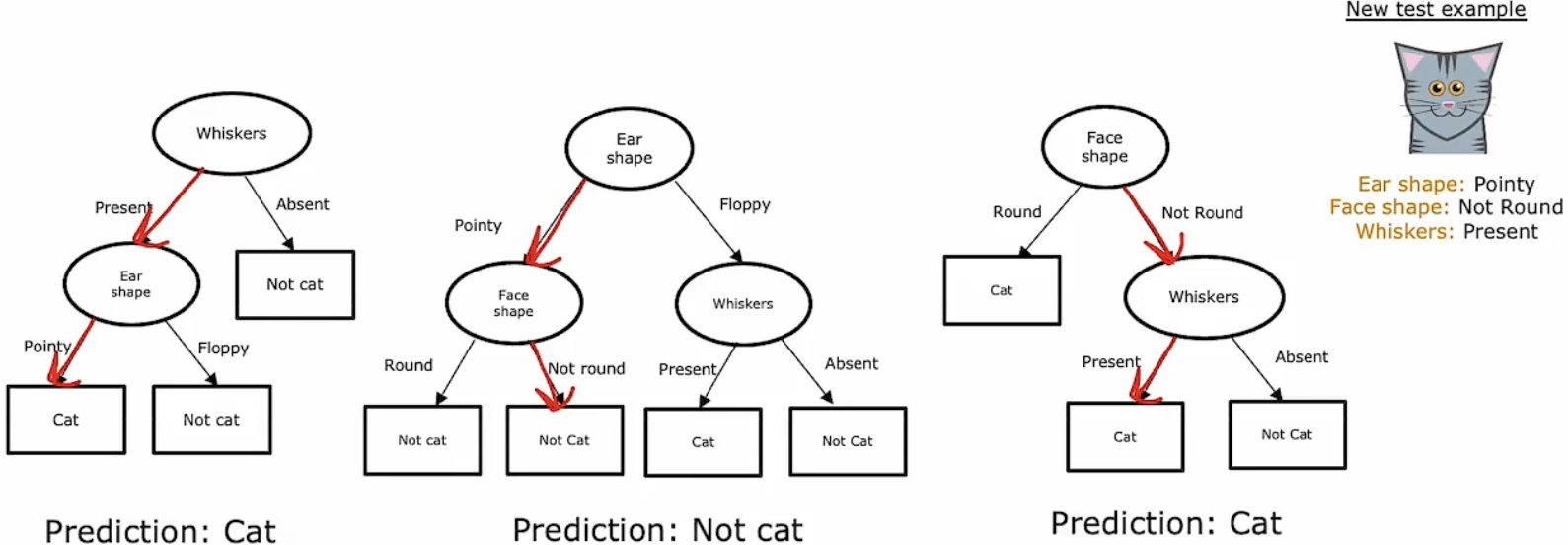
这样，对于想要预测的例子不同的决策树会产生不同的预测结果，最后我们可以通过“投票”的方式投选出正确的结果。通过这种方式我们的决策树会更加健壮。

有放回抽样

前面，我们说到，我们想要构建多个决策树来使我们的代码更加的“健壮”。那么通过什么样的方式构建这样的决策树集合呢？这里需要用到的技术叫做“有放回抽样”。

那么什么是有放回抽样呢？

相信我们在学习大二学习概率与统计的时候接触过这个概念，就是从一个集合中随机挑选一个样本记录下来，然后将此样本放回该集合，重新抽样，重复此过程。这个过程中我们或许会抽到相同的样本，也或许会完全不同。

将有放回抽样用在猫的例子中如下图所示：

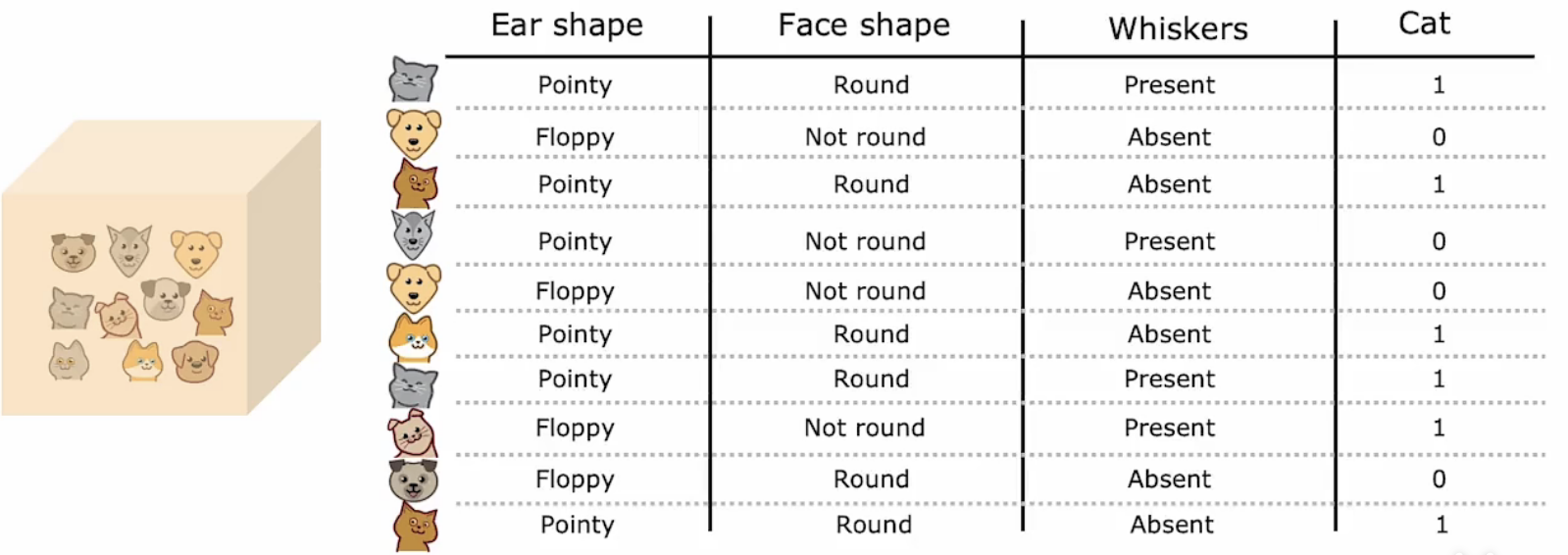
我们利用有放回抽样产生的数据集训练，从而产生一个决策树集合。

随机森林

在讲述随机森林之前，我们重新描述一下建立决策树集合的过程。

对于一个包含M个样本的样本集，进行B轮有放回抽样，对于每一轮的有放回抽样，我们利用抽样得到的数据集训练决策树模型，最终得到一个又B个决策树模型组成的决策树集合。其中需要注意的是，B的取值并不是越大越好，当B达到某一个数值时，继续增加B只会减慢训练速度，但决策树模型的预测效果并不会显著提高。

另外，在实际训练的过程中可能会出现一个问题，那就是即使进行了有放回抽样，但最终得到的多个决策树模型可能根节点特征都相同或者大部分相同，或者说决策树模型重合度较高。这种情况就不符合我们的初衷。

所以我们将算法进一步修改，增加随机性，也就成了所谓的随机森林。

随机森林：如果存在M个特征，则在每个节点分裂的时候，从M中随机选择m个特征维度（m << M，在视频中m=$\sqrt{M}$），使用这些m个特征维度中最佳特征(最大化信息增益)来分割节点。在森林生长期间，m的值保持不变。（这点课上由于翻译问题没有听懂，去查了知乎的一个解释，链接在此：[机器学习基础复习] 随机森林(Random Forest) - 知乎 (zhihu.com)）

XGBoost

在决策树集成算法的领域中有一个常用于机器学习竞赛、商业领域的算法，那就是XGBoost(Extreme Gradient Boosting),这种算法具有运行速度快，开源易使用的特点。

我觉得XGBoost是一种改进的随机森林，他的基本原理与随机森林基本相同，有一点不同的地方是在随机森林中我们提到：

对于一个包含M个样本的样本集，进行B轮有放回抽样，对于每一轮的有放回抽样，我们利用抽样得到的数据集训练决策树模型，最终得到一个又B个决策树模型组成的决策树集合。

而在XGBoost中，同样是对于一个包含M个样本的样本集，进行B轮有放回抽样。但对于每一轮的有放回抽样，我们有更高的概率抽到之前模型验证错误的例子进入此轮的有放回抽样当中去，之后利用抽样得到的数据集训练决策树模型。最终我们得到一个由B个决策树模型组成的决策树集合。

在我进一步去搜索相关XGBoost的内容时，发现在基本原理的背后还有一些高深的数学知识的支持，涉及到了正则化、泰勒级数展开等等等等。这些学会这些数学基础更有利于我们去学习算法知识，不过在本视频阶段暂且不讨论背后的数学原理了，等下一阶段可以再深入了解。

决策树 vs 神经网络

此处讲一下决策树以及神经网络的好处，包括在何种情况下使用何种方法更好。

对于决策树：

1.决策树在处理结构化的表格数据时表现更加优秀，非结构化的数据如文本、视频、语音不太擅长。

2.训练速度快

3.小的决策树有助于人类思维的理解。

对于神经网络：

1.对于所有类型的数据均适用，包括结构化的表格数据、文本、视频、语音等等。

2.训练时可能会比决策树速度慢。

3.可以与迁移学习联用。

4.当想要构建一个由多个模型一起工作的系统时，联接多个神经网络在技术上更容易实现。

---

到这里监督学习部分就结束了🥳🥳，下面的内容是无监督学习部分。

庆祝一下，分享一个吴恩达老师上课时候讲的笑话：

问：机器学习工程师在哪里露营？？

答：在随机森林里🤣

---

聚类算法（Clustering）

聚类算法是一种典型的无监督机器学习，与监督学习不同的是，无监督学习只有数据而没有数据标签。聚类算法所要做的就是在无标签的情况下寻找数据的结构特点（这种结构特点类似于一种标签，但实际并无标签），并将具有相似结构特点的数据分类在一起。下面两张图揭示了无监督学习中数据集的数据特点：

监督学习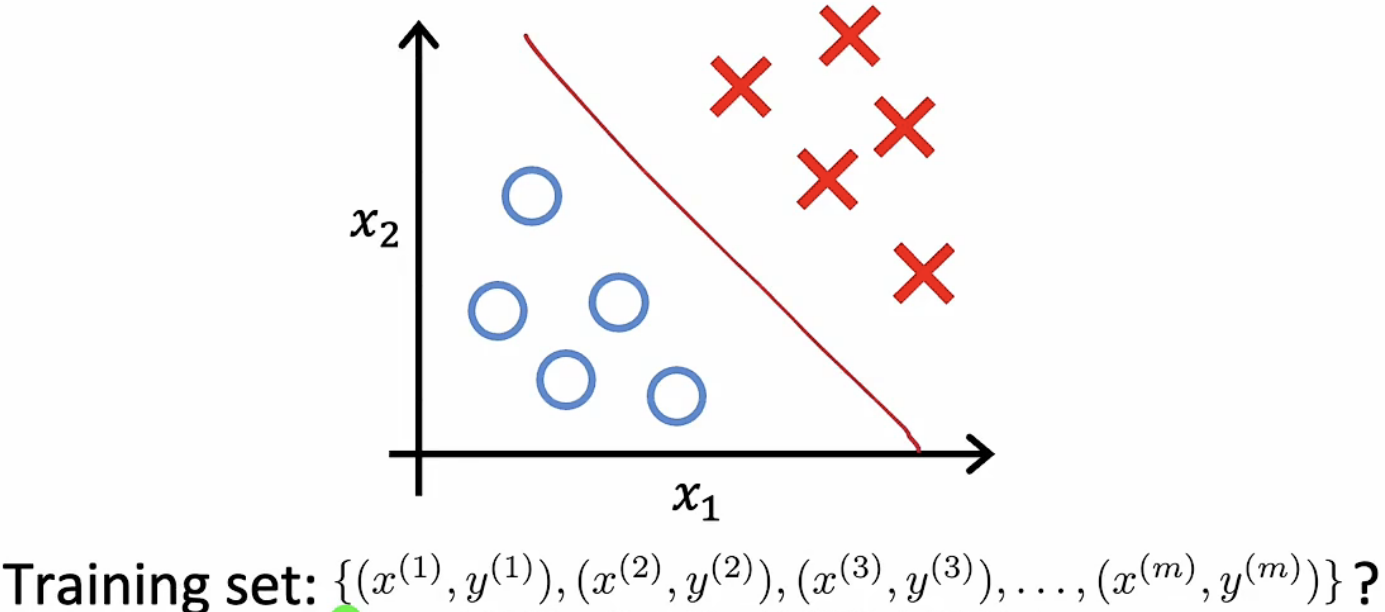	无监督学习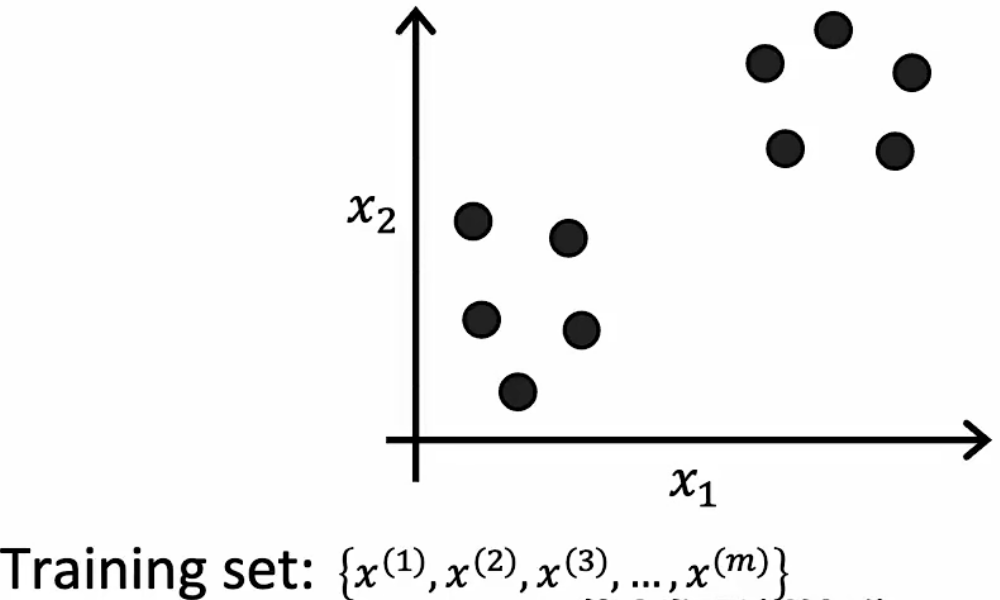

聚类算法常常用于新闻以及商业广告的推荐、各种活动中目标人群的分类、DNA数据特征分析甚至包括天文学数据分析等等。

K-means的直观理解

这节我们简单介绍一下聚类算法中最常用的算法——K-means算法。

K-means算法的工作原理主要分为两步：

准备：在开始前我们随机在坐标中图中找基准两个点。

第一步：接着计算数据集中的每个点距两个基准点之间的距离，并将数据点与其距离更近的那个基准点归为一类。

第二步：遍历完所有数据点后，计算归属到同一基准点的所有数据点的平均值，标注在坐标图上。

最后：重复第一步

重复n次后：基准点收敛到某一处，分类完成，距离某个基准点距离最近的数据子集为一类。

为了更直观的理解这个过程，我们可以参考以下图组：

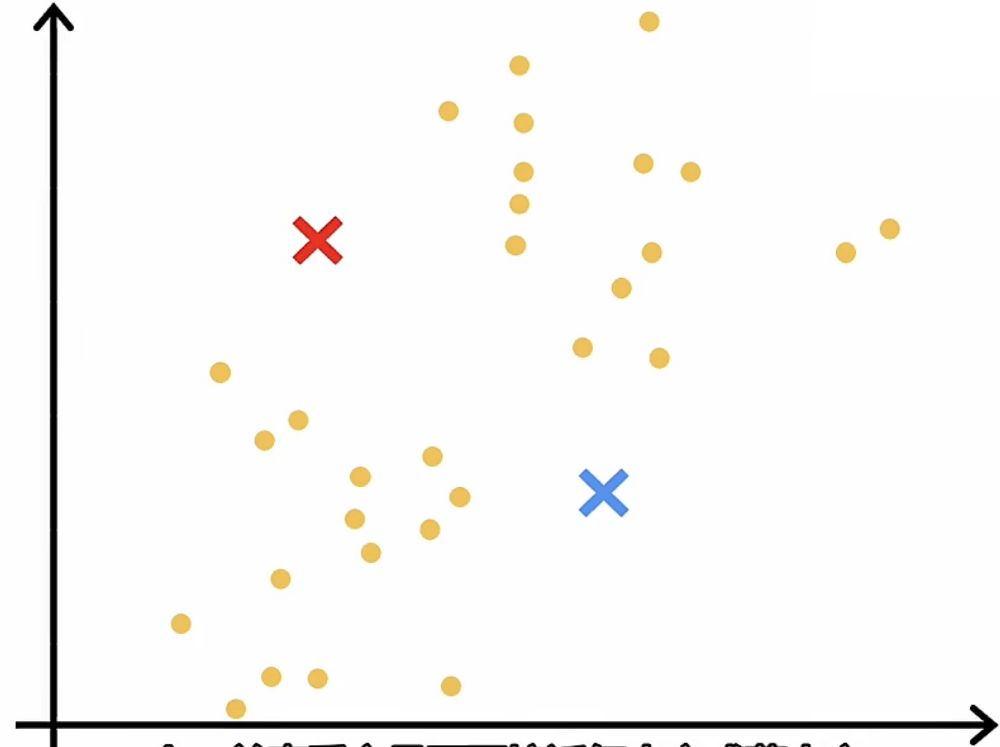	在坐标中随机找两个集群中心，图中标注为红色和蓝色
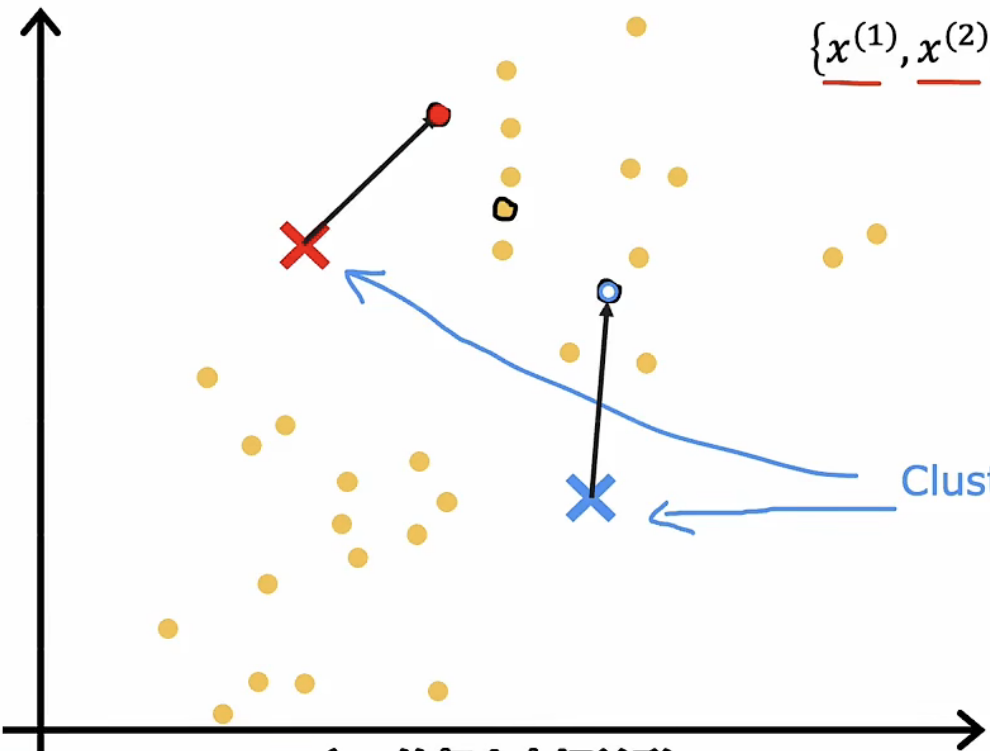	遍历每一个数据点，计算该数据点与两个集群点之间的距离，将其归属为与其距离最相近的集群点。这里我们将该数据点染红表示归属为红色集群点
	计算归为一类的所有数据点的均值，并将新的集群点刷新至该均值。
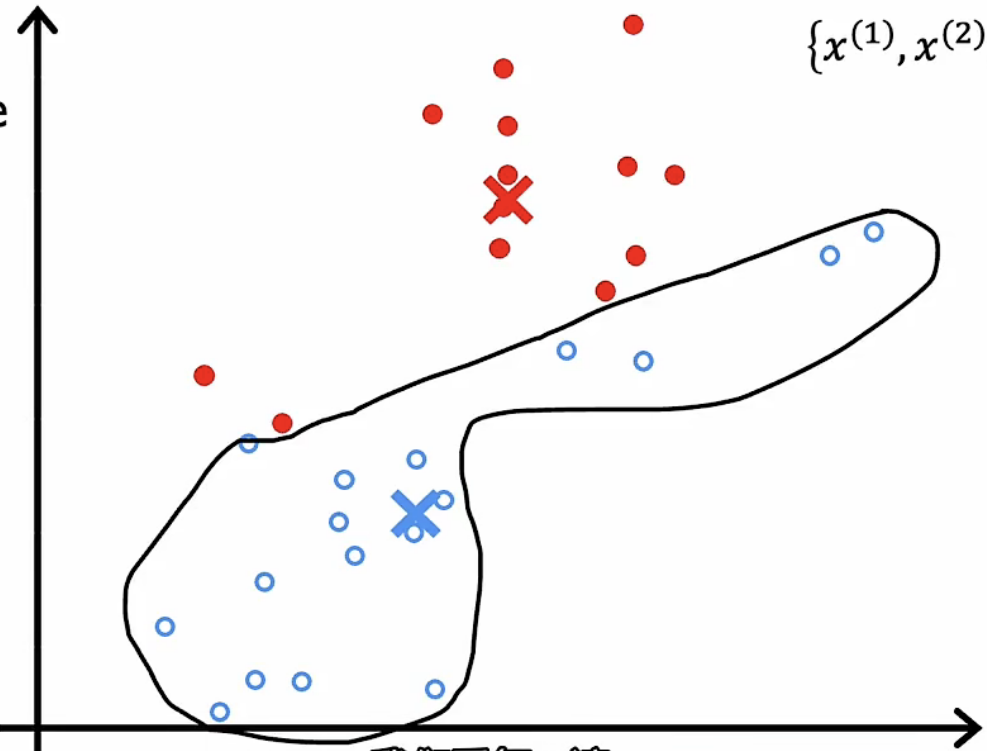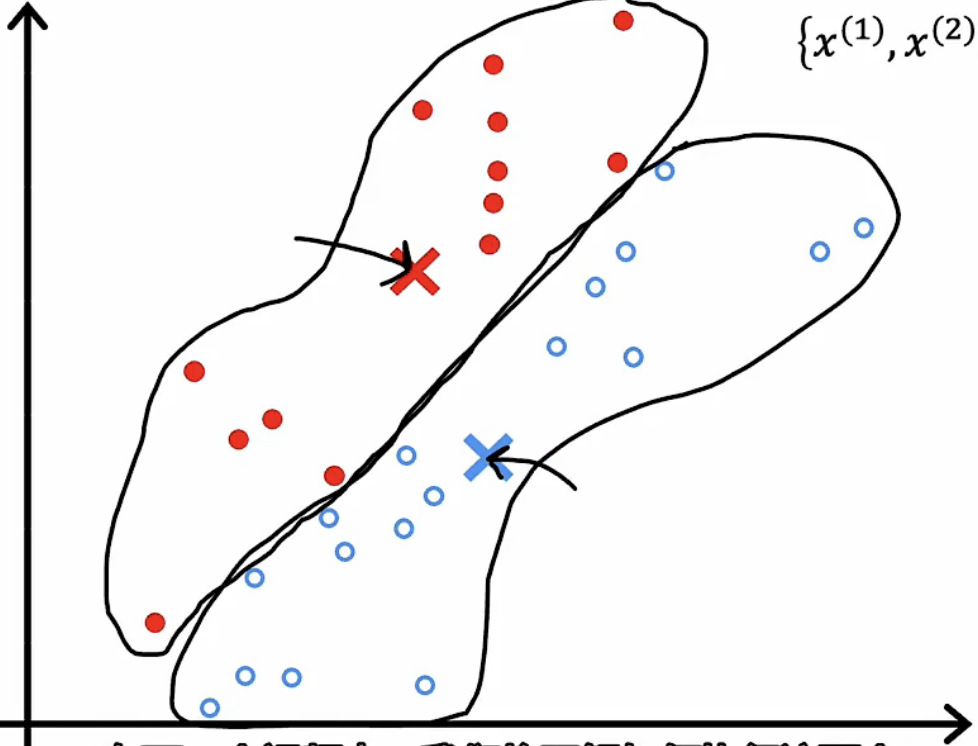
	遍历每一个数据点，将其归属为与其距离最相近的新的集群点。这里我们将该数据点染红表示归属为红色集群点。计算归为一类的所有数据点的均值，并将新的集群点刷新至该均值。
·····	重复上述步骤
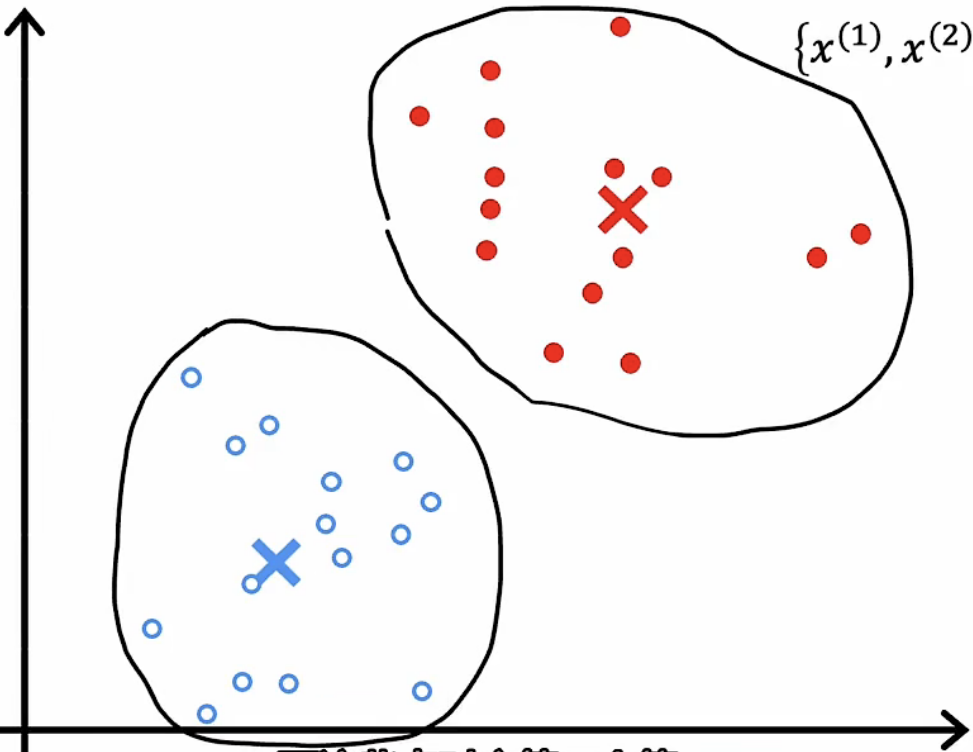	最终，集群点收敛，距离某个基准点距离最近的数据子集为一类。

k-means算法

本节中我们介绍一些k-means算法的一些符号表示以及算法的伪代码。下面是视频中的伪代码

Randomly initialize K cluster centroids μ1,μ2，...,μk∈R^n
Repeat{
		for i=1 to m
			c^(i): =index(from 1 to K) of cluster centroid closest to x^(i)
			//c^(i)表示对于第i个数据点，其与第K个集群点的距离最小的K值，可以表示为 min_k|c^(i) - μk| ,这里我们由于习惯统一规定为 min_k(|c^(i) - μk|^2 )
			//即对于c^(2),若μ3距离其最近，那么c^(2) = 3
            for k=1 to K
			μk: =average(mean) of points assigned to cluster k
			//μk表示属于μk集群中所有数据点的平均值
			//若c^(2)，c^(3)，c^(4)，c^(10)距离μ5很近，那么μ5 = {c^(2)+c^(3)+c^(4)+c^(10)}/4
}			

首先随机初始化集群点，并标记为μ1,μ2，…,μk，其中下标K代表K个集群点。

接着进入重复循环

{

在循环中，我们所做的第一件事就是遍历每个数据点，找到与其最相近的集群点并表示出对应的c^(i)的值。

在循环中，我们需要做的第二件事是在遍历完所有数据点后，将属于同一个 μk的所有数据点的值进行平均处理并赋值给对应的μk。

}

k-means目标优化函数

在讲述监督学习时，无论是线性回归、多元线性回归、逻辑回归等都有一个目标优化函数，即成本函数。成本函数主要用于帮助我们找到更优情况下的模型。与监督学习相同，无监督学习同样也有目标优化函数。在本节中，我们将讨论关于K-means的目标优化函数。

我们已经知道：

$c^{(i)}$: = index (from 1 to K) of cluster to which example $x^{(i)}$ is currently assigned

$μ_k$: = cluster centroid k ($μ_k$∈$R^n$)

$μ_{c^{(i)}}$: = cluster centroid of cluster to which example $x^{(i)}$ has been assigned

根据这些特殊符号，我们可以定义目标优化函数如下：

$$J(c^{(1)},...,c^{(m)},μ_1,...,μ_k) = \frac{1}{m}\sum_{i=1}^{m}||x^{(i)} - μ_{c^{(i)}}||^2\tag{4.3}$$

这里需要提到的一点是在算法中，我们所做的两个重复步骤都是在最小化目标函数

Randomly initialize K cluster centroids μ1,μ2，...,μk∈R^n
Repeat{
		for i=1 to m
			c^(i): =index(from 1 to K) of cluster centroid closest to x^(i)
			
        for k=1 to K
			μk: =average(mean) of points assigned to cluster k
			
}			

在重复段的第一个任务中，我们事实上在最小化目标优化函数，途径主要是通过将数据点划分给离他最近的那个集群簇，这样使得$||x^{(i)} - μ_{c^{(i)}}||^2$的值最小。而在第二个任务中，我们同样也是在最小化目标函数，只不过这次主要是通过平均属于他的数据点的值，将此值作为移动后集群簇点$μ_{c^{(i)}}$位置，最终实现此集群簇点距离归属其下的所有点距离最近。两个任务目标相同，第一个任务是相对于$c^{(1)},c^{(2)},…,c^{(n)}$而言，第二个任务是相对于$μ_{1},μ_{2},…,μ_{n}$而言。

k-means的初始化与聚类数量选择

k-means初始化

在前几节课中，我们提到k-means的集群点在初始化的时候是随机初始化。但在实际情况中，我们通常是将集群点初始化为数据集中任意k个数据。这种方法在实际使用的过程中无法避免的也会出现问题，因为当集群点随机为不同的数据点时，最后的分类结果可能会不同，无法达到我们想要的效果。

为了解决这个问题，我们通常是进行n次随机选择，n取50-1000。每次随机初始化都进行k-means分类操作并计算目标优化函数值，最后选择目标优化函数值最小的那个初始化结果。

但这里需要注意的一点是这种多次随机选择能够显著改善结果的的方法仅仅适用于k值很小的情况，当k值很大的时候，即使增加随机选择的次数，分类的效果不会有太大的改善。

聚类数量选择

关于聚类数量的选择，我们无法给出一个固定的答案来说明到底有几个集群，因为有的人认为可以分成两个，而有的人认为可以分成三个、四个等等。因此，现在还并没有一种较为智能和自动化的方法来找出聚类数量，一般是通过手动设置聚类数量观察分类后的特征。常用的一种手动选择方法被称作为 “ 肘部方法（Elbow method）”。

Elbow method：先手动设置聚类的数量，然后绘制出成本函数关于聚类数量的函数图，在图中找出函数拐点，将此拐点处的所代表的聚类数量作为最优解，如下图所示:

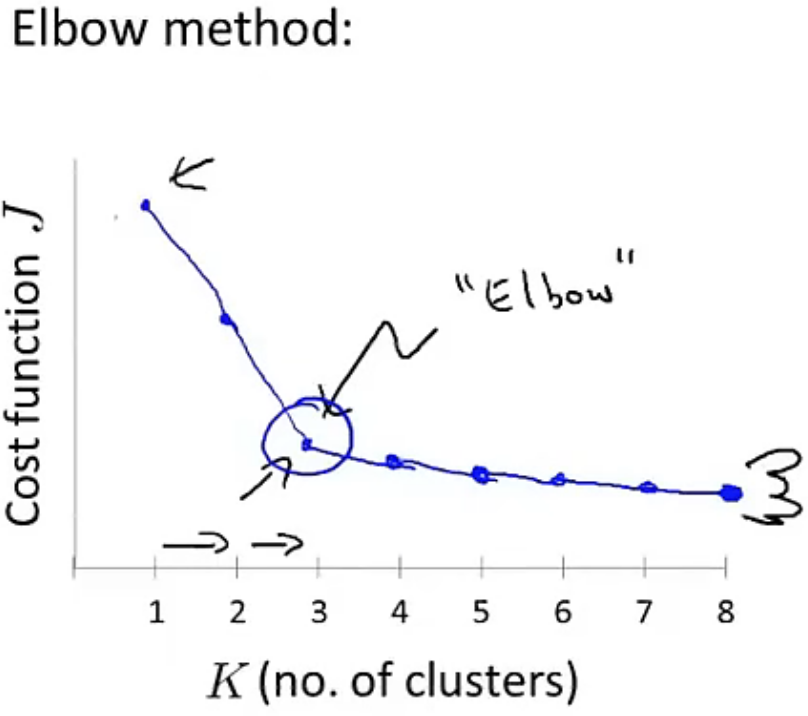
上图显示的最优聚类数量为3。这里我们需要注意，Elbow method的适用范围实际是很窄的，它并不能解决所有聚类问题。因为在实际应用中，我们常常遇到的是更为平滑的曲线，而不是上图中的折线。但总的来说，这种方法依然值得我们去尝试。

那再实际应用的过程中我们到底该如何选择聚类数量呢？Andrew老师给出了一个宽泛的答案，那就是根据我们的应用场景选择合适的数量， 比如在不同身高不同体重的人该划定到什么样的衣服尺寸的情境下，我们如何划分衣服尺寸呢？是分为三类（S\M\L），还是五类（XS\S\M\L\XL）,哪一类能更加满足客户的多样化需求呢？这就是根据应用场景与需求来划分聚类数目的小例子。

降维问题（Dimentionality Reduction）

降维是无监督学习算法的一种，常常用于内存、硬盘等存储区域的内存压缩，机器学习算法的加速。

什么是降维？

降维，根据字面意思我们就可以理解，即将高维数据进行数据处理，从而使得我们可以利用低维数据来表示高维数据，如从2维数据降到1维数据，从3维数据降到2维数据，从10000维数据降到100维数据，降维后的数据与降维前的数据是一种一一映射的关系。

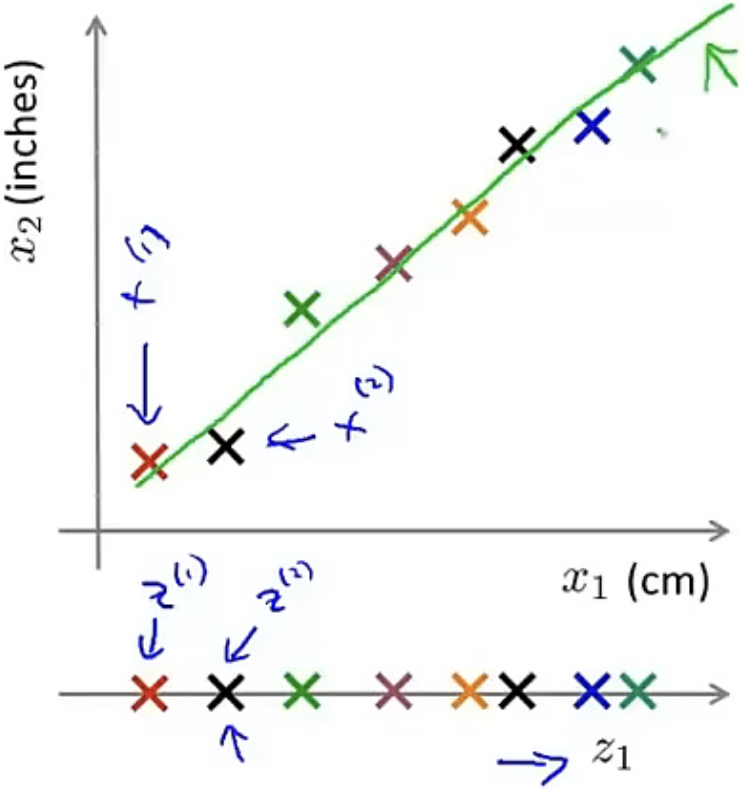	2D -> 1D: 降维前我们使用$x^{(1)}$,$x^{(2)}$,….,$x^{(n)}$来表示数据点，且$x^{(1)}$,$x^{(2)}$,….,$x^{(n)}$∈$R^2$；降维后我们用$z^{(1)}$,$z^{(2)}$,….,$z^{(n)}$来代表每个数据点，且$z^{(1)}$,$z^{(2)}$,….,$z^{(n)}$∈$R$。
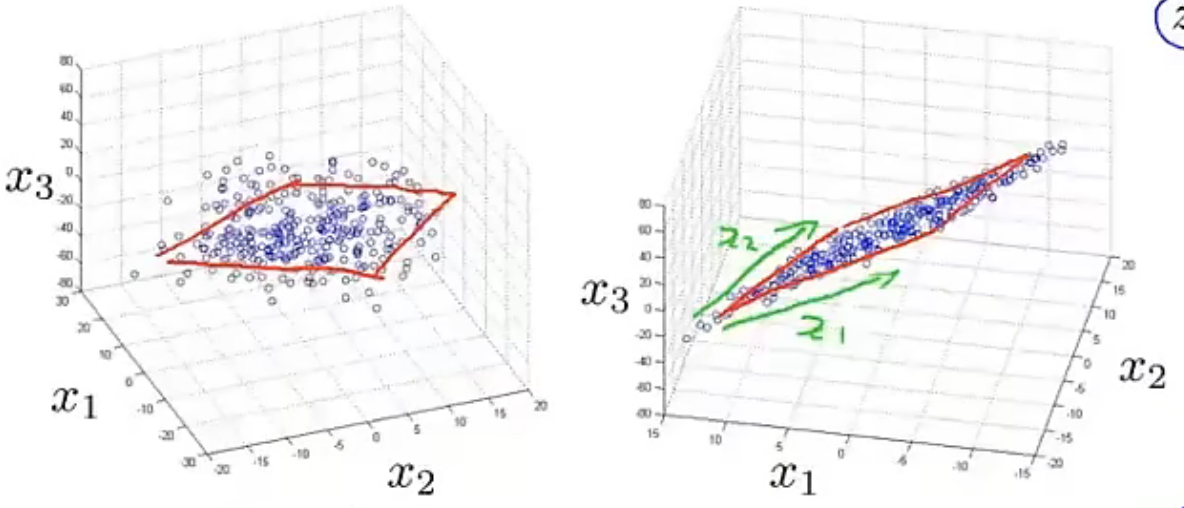	3D -> 2D: 降维前我们使用$x^{(1)}$,$x^{(2)}$,….,$x^{(n)}$来表示数据点，且$x^{(1)}$,$x^{(2)}$,….,$x^{(n)}$∈$R^3$；降维后我们用$z^{(1)}$,$z^{(2)}$,….,$z^{(n)}$来代表每个数据点，且$z^{(1)}$,$z^{(2)}$,….,$z^{(n)}$∈$R^2$。

上图组可以帮助我们理解降维算法是如何帮助我们压缩数据的，用一维数据来表示二维数据可以实现数据压缩效果。但这里Andrew老师并没有深入讲解降维算法如何是实现内存数据的压缩，所以我还有一些疑问没有解决：这种压缩是否类似于我们使用计算机时常常会用到的压缩包，可以将文件大小大大减小？降维处理后的数据还能反映出原数据的特点？这里先继续学习下面的内容，看后续是否会讲到

降维算法除了可以进行数据的压缩，他的另一个应用是数据可视化。

数据可视化

降维算法常常用于帮助我们数据可视化从而帮助我们优化机器学习算法。

假如我们现在有以下数据，数据中所表示的是各国的GDP,人均GDP等等数据，是一个50维数据。

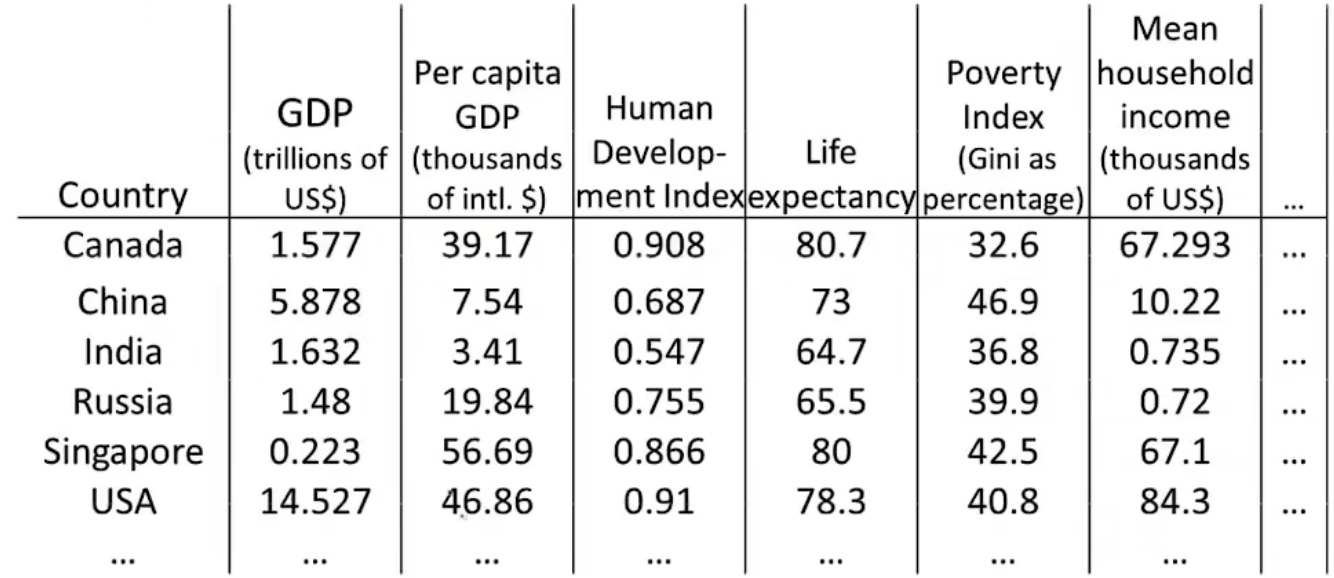
通过降维算法后，假设我们可以将数据从50维压缩到2维数据，得到如下图所示数据

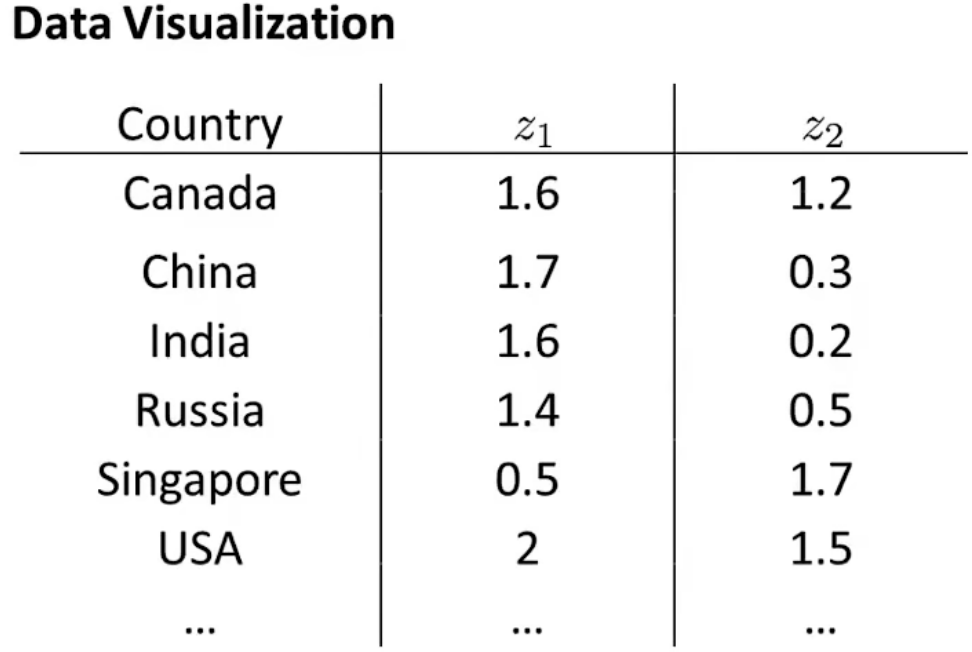
可能有人会有疑问：我通过降维处理后的数据有什么意义呢，他所表示什么含义呢？

Andrew给出的答案是：通常情况下，经过降维处理后的数据通常不具有什么物理意义，但我们可以通过将这些点在二维坐标中表示出来如下：

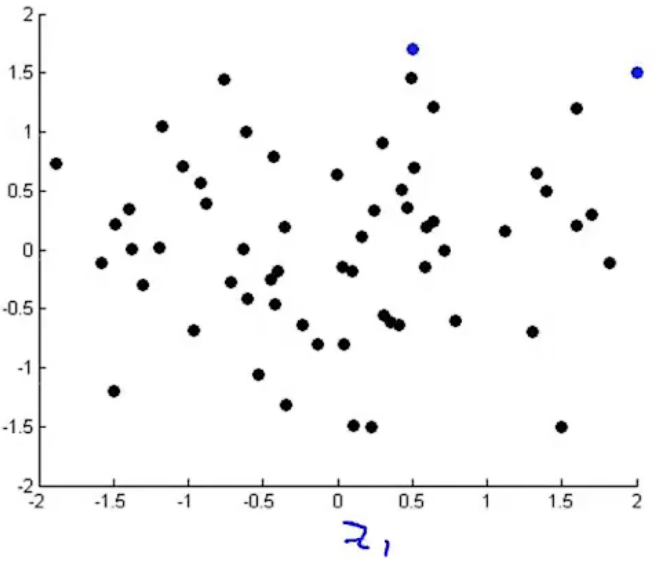
通过将这些坐标点可视化处理可以帮助我们理解降维后数据的意义，如横轴相当于一个国家总体规模或者国家总体经济活跃程度，纵轴就大致相当于人民的幸福指数，人均GDP等等数据。但这里Andrew老师并没有指出这些意义是在降维后人为赋予的意义，还是我们在处理数据时将五十维的数据带入某个数学模型后输出的结果作为

异常检测算法（Anomaly Detection）

异常检测算法是一种无监督学习算法，他常常用来检测某个数据是否异常，多应用于金融、制造业等领域。在制造业领域，我们可以用异常检测算法来检测某个制造商所生产的产品是否合格，如一个新生产的飞机发动机的参数（放热、强度）是否正常，若正常则可出售，若不正常可需返工。在金融领域，我们可以通过检测某个账户的流水来判断某笔交易是否具有风险。

异常检测算法的原理是依据数学中的高斯模型建立的，先利用大量数据来建立一个高斯模型，再将测试数据带入该高斯模型中，将带入模型后所得到的概率结果与我们所设置的阈值进行比较，从而完成对测试数据的质量评估。

异常检测算法实现

前面已经提到，异常检测算法的实现主要是依靠高斯数学模型，而在高斯模型中有两个重要的参数，一个是平均值 $μ$，另一个则是 $σ$ 。下面我们先列出高斯模型的数学表达式，关于更为详细的高斯模型知识这里暂不赘述。

$$p(x)=\frac{1}{\sqrt{2Π}σ}e^{\frac{-(x-μ)^2}{2σ^2}} \tag{4.4}$$

对于一维数据，我们清楚如何求解对应的$μ$、$σ$。

但现实情况下，数据往往是多维的，那如何在多维数据下建立高斯数学模型呢？

对于多维数据的处理，我们通常会先计算每一维数据对应的概率，再将所有概率依次相乘得到最终结果。

$$对于第j维的数据： μ_j=\frac{1}{m}\sum_{i=1}^mx_j^{(i)}\tag{4.5}$$ $$对于第j维的数据： σ_j^2=\frac{1}{m}\sum_{i=1}^m(x_j^{(i)}-μ_j)^2\tag{4.6}$$

在计算完所有维数的概率后，将其相乘得到最终结果，公式如下：

$$p(x)=\prod_{j=1}^np(x_j;μ_j,σ_j^2)=\prod_{j=1}^n\frac{1}{\sqrt{2Π}σ_j}exp({-\frac{(x_j-μ_j)^2}{2σ_j^2}})\tag{4.7}$$

最后再将$p(x)$与阈值 $\varepsilon\$比较从而判断该产品的参数是否异常，若$p(x)$大于等于阈值 $\varepsilon\$，标记为正常，若$p(x)$小于阈值 $\varepsilon\$，标记为异常。

异常检测与监督学习算法对比

在讲述监督学习时，我们曾提到过判断一个邮件是否是垃圾邮件的例子，同样也可以理解为是一种检测异常的方式。那么监督学习的检测与异常检测有何区别呢？

	异常检测	监督学习
特点	异常检测训练集中的正例（异常点）相对于负例（正常情况）很少甚至没有，正例仅仅用于交叉验证及测试集；在异常检测的训练中，我们往往仅训练所有负例，根据已有的负例特征判断未来例子的异常情况；异常检测算法的异常点往往是我们预想不到的，或与以前所有异常点都不一样的例子。	监督学习的训练集中，正例负例都很多；在进行监督学习时的训练时，我们会将正例与负例一起训练；监督学习算法中，我们默认未来出现的例子异常点会与已出现的异常点类似。
例子讲解	如在金融诈骗时，诈骗手段往往是不断更新的，我们无法将其作为一种正例来进行监督学习，因为当有新手段时，监督学习的训练集中仅仅包含了上次的旧手段，无法更好的识别这次的新手段，即使再将这次的新手段放入训练集，下次还会出现更新的手段，因此可能永远无法用监督学习来辨别诈骗手段。这时我们便需要使用异常检测来进行更好的判断。	在辨别垃圾邮件时，由于往往遇到相同类型的垃圾邮件，新型垃圾邮件很好出现或者说迭代的并不频繁，因此处理垃圾邮件时我们可以选择监督学习，将已知类型的垃圾邮件特点放入训练集，监督学习算法便可以很好的分辨这些垃圾邮件。

推荐系统

推荐算法是一种常用的机器学习算法，其被广泛地应用于商业中。在生活中，我们会接触许多推荐系统，如网购时，我们总能在特定区域找到与该物品类似的商品。在阅读新闻时，与正在阅读的新闻类似的其他新闻也会推送给用户。在视频网站（如YouTube），用户也会被推送可能与其喜好相一致的电影。包括我们所熟知的短视频App（如抖音、快手）都会推送你可能感兴趣的短视频。由此可见，生活中处处都有推荐系统。本节我们将会利用电影网站的例子来讲述一些推荐系统算法与优化。

在电影网站中，对于网站的推荐系统来说，我们常常会接触到系统为你推送的 “评分环节” 以及系统为你推荐的 “你可能喜欢的电影”。而对于观影的我们，我们一般会根据自己的喜好来看电影。对于电影本身，不同的电影会被贴上不同的标签，如爱情类电影、动作类电影、冒险类电影等等。

待更新..

强化学习

强化学习是机器学习的支柱之一，但还未广泛应用于商业活动中。生活中，强化学习算法常用于机器人（包括近期火热的机器狗等等）、航空航天器控制，工厂生产、金融股票、智能棋类、游戏等领域。

在视频中，老师先展示了一个斯坦福研发的基于强化学习的自动直升机视频，看完后感觉很奇特，分享如下：

	开始时，只是一个平平无奇的直升飞机
	直升飞机上面出现了树，依然有点懵
	直到镜头将直升飞机放在大背景下，震惊！在倒飞

这个直升飞机倒飞的特技是通过强化学习实现的，感觉很奇特，很有意思。

那什么是强化学习呢？

与监督学习不同，强化学习没有大量的正面数据与负面数据构成的数据集来用于训练模型（我们也不可能搜集得了所有的直升飞机应有的正面数据特征），而是通过类似于人类训练修狗狗一样的方法：在修狗做的好时，我们会说：好狗狗！并给予好吃的进行奖励；当修狗做的不好时，我们会说：坏狗！给予训斥。通过强化学习训练直升机时，我们也可以在直升机飞行稳定、灵敏调节等情况下进行奖励，好直升飞机！而在坠毁等失误后进行惩罚，坏直升飞机！——吴恩达如是说😂。

因此，对于强化学习，我们不需要像监督学习一样告诉直升机每个输入的正确输出y是什么（我们也无法搜集的完所有输入与输出数据，因为直升机的状态情况过于复杂）。而是需要做的是建立奖励函数，告诉直升机什么时候做的好，什么时候做的不好。

强化学习的回报